Light is a transverse electromagnetic wave. The electric field of an electromagnetic plane wave is of the form
E(r,t) = Emaxcos(k×r-wt+f), Emax ^ k.
The electric field of an EM plane wave traveling in the x-direction therefore may be written as
E(x,t) = Emaxcos(kx-wt+f), Emax ^ i.
If we consider a linearly polarized plane wave and we orient our coordinate system so that Emax is directed along the y-axis then we can drop the vector notation and write
E(x,t) = Emaxcos(kx-wt+f), E = Ey.
A more convenient notation is complex notation. For any angle q,
cosq = Re(exp(iq)), exp(iq) = cosq + i sinq.
We therefore rewrite the above equation as
E(x,t) = Emax exp(i(kx-wt+f)), E = Ey.
When we use complex notation to specify the electric field of an electromagnetic wave, it is implied that only the real part of the equation describes the electric field.
Two or more waves traveling in the same medium travel independently and can pass through each other. In regions where they overlap we only observe a single disturbance. We observe interference. When two or more light waves interfere, the resulting electric field amplitude is equal to the vector sum of the individual field amplitudes. If two waves with equal amplitudes are in phase and overlap i.e. if crest meets crest and trough meets trough, then we observe a resultant wave with twice the amplitude. We have constructive interference. If the two overlapping waves, however, are completely out of phase, i.e. if crest meets trough, then the two waves cancel each other out completely. We have destructive interference.
Let us add two linearly polarized plane electromagnetic waves with equal wavelengths but different phases, traveling along the x-axis.
E1(x,t) = A1 exp(i(kx-wt+f1)), E2(x,t) = A2 exp(i(kx-wt+f2)),
E(x,t) = E1(x,t) + E2(x,t) = (A1 exp(if1) + A2 exp(if2)) exp(i(kx-wt))
= AR exp(i(kx-wt+fR)).
The result of the addition is a linearly polarized plane electromagnetic waves with the same wavelength but a different phase and amplitude, traveling along the x-axis.
Here AR is the resultant amplitude and fR is the resultant phase.
A1 exp(if1) + A2 exp(if2) = AR exp(ifR)
To find the magnitude of a complex number we multiply the number by its complex conjugate and then take the square root. The square of the resultant amplitude is given by
AR2 = (A1 exp(if1) + A2 exp(if2))(A1 exp(-if1) + A2 exp(-if2))
= A12 + A22 + A1A2(exp(i(f1-f2)) + exp(-i(f1-f2)))
= A12 + A22 + 2A1A2cos(f1-f2).
The intensity of a wave is proportional to the square of its amplitude. The intensity of the resultant wave is therefore proportional to AR2.
To find fR we use
tanfR = (A1 sinf1 + A2 sinf2) / (A1 cosf1 + A2 cosf2)
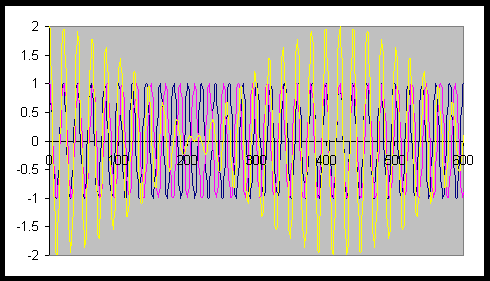
Let us add two linearly polarized plane electromagnetic waves with equal amplitudes but slightly different wavelengths and therefore different frequencies. (w/k = c/n.)
E1(x,t) = A exp(i(kx-wt)), E2(x,t) = A exp(i((k+dk)x-(w+dw)t)),
E(x,t) = E1(x,t) + E2(x,t) = A exp(i(kx-wt))(1 + exp(i(dk x - dw t)))
= A exp(i(kx-wt)) exp((i/2)(dk x - dw t)) 2cos((dk x - dw t)/2)
= 2A exp(i((k+dk/2)x - (w + dw/2)t)) cos((dk x - dw t)/2).
We obtain a traveling wave exp(i((k+dk/2)x-(w+dw/2)t)) with the average frequency of the two waves being added with an amplitude 2A cos((dk x - dw t)/2). The amplitude itself is a traveling wave, traveling with speed vg = dw/dk.
We call vp = w/k = c/n the phase velocity of the waves and vg = dw/dk the group velocity. For electromagnetic waves in empty space vp = vg = c. If we have dispersion in a material and the index of refraction n = n(k), the the group and phase velocity are not equal to each other.
The two waves in the figure above have wavelengths of 20 and 21 units respectively. Their frequencies are v/20 and v/21, where v is the speed of the waves. The frequency of the intensity variations is v/20 – v/21 = v/420.
Link:
 | Exploring Interference (a spreadsheet) |
What if the beams do not travel in the same direction?
The double slit (interference by division of wavefront)
Interference patterns are only observed if the interfering light from the various sources is coherent, i.e. if the phase difference between the sources is constant. Splitting the light from a single source into various beams guaranties coherence as long as the optical path lengths are nearly equal. Light from two different light bulbs is incoherent and will not produce an interference pattern. Lasers are sources of monochromatic, (single wavelength), coherent light. Two lasers can maintain a constant phase difference between each other for relatively long time intervals or for relatively large path-length differences.
A scheme for thinking about the nature of wave propagation is called Huygen's principle. If light from a distant point source is incident onto an obstacle which contains two very small slits a distance d apart, then the wavelets emanating from each slit will constructively interfere behind the obstacle.
If we let the light fall onto a screen behind the obstacle, we will observe a pattern of bright and dark stripes on the screen. This pattern of bright and dark lines is known as a fringe pattern. The bright lines indicate constructive interference and the dark lines indicate destructive interference.
The bright fringe in the middle of the diagram above is caused by constructive interference of the light from the two slits traveling the same distance to the screen. It is known as the zero-order fringe. Crest meets crest and trough meets trough. The dark fringes on either side of the zero-order fringe are caused by destructive interference. Light from one slit travels a distance that is 1/2 wavelength longer than the distance traveled by light from the other slit. Crests meets troughs at these locations. The dark fringes are followed by the first-order fringes, one on each side of the zero-order fringe. Light from one slit travels a distance that is one wavelength longer than the distance traveled by light from the other slit to reach these positions. Crest again meets crest.
The diagram shows the geometry for the fringe pattern. We assume L >> d. If light with wavelength l passes through two slits separated by a distance d, we will observe constructively interference at certain angles. These angles are found by applying the condition for constructive interference, which is
d sinq = ml, m = 0, 1, 2, ….
The angles at which dark fringes occur can be found be applying the condition for destructive interference, which is
d sinq = (m+1/2)l, m = 0, 1, 2, ….
If the interference pattern is viewed on a screen a distance L from the slits, then the wavelength can be found from the spacing of the fringes. We approximately have sinq = z/L and
l = zd/(mL),
where z is the distance from the center of the interference pattern to the mth bright line in the pattern. This applies as long as the angle q is small, i.e., as long as z is small compared to L.
Links:
| Double slit interference |
| Physics 2000: Wave Interference |
What happens when light encounters an entire array of identical, equally-spaced slits, called a diffraction grating?
The bright fringes, which come from constructive interference of the light waves from different slits, are found at the same angles they are found if there are only two slits. But the pattern is much sharper. Why?
For two slits, there is one single position between bright peaks, where the interference is totally destructive. Between the zero-order and first-order fringes, there is one position which requires that one of the waves travels exactly 1/2 wavelength further than the other to reach it. For three slits, however, there are two positions where destructive interference takes place. One is located at the point where the path lengths differ by 1/3 of a wavelength, while the other is located where the path lengths differ by 2/3 of a wavelength. For 4 slits, there are three positions, for 5 slits there are four positions, etc. For a diffraction grating with a large number of slits, the pattern is sharp because of the many positions of completely destructive interference between the bright, constructive-interference fringes.
Diffraction gratings, like prisms, disperse white light into its component colors. The spectral pattern is repeated on either side of the main pattern. These repetitions are called "higher order spectra". There are often many of them, each one fainter than the previous one. If the distance between slits is d, and the angle to a bright fringe of a particular color is q, the wavelength of the light can be calculated.
Problems:
| The first order bright line appears 0.25 cm from the center bright line when
a double slit grating is used. The distance between the slits is 0.5
mm and the screen is 2.7 m from the grating. Find the wavelength.
| ||
| A diffraction grating has 420 lines per mm. The grating is used to
observe light with a wavelength of 440 nm. The grating is placed 1.3 m
from the source. Where will the first order bright line appear?
|
Thin-film interference (interference by division of amplitude)
When a light wave reflects from a medium with a larger index of refraction, then the phase shift of the reflected wave with respect to the incident wave is p (180o). When a light wave reflects from a medium with a smaller index of refraction, then the phase shift of the reflected wave with respect to the incident wave is zero. When a light wave is reflected, the reflected and the incident wave interfere.
Constructive and destructive interference of reflected light waves causes the colorful patterns we often observe in thin films, such as soap bubbles and layers of oil on water. Thin-film interference is the interference of light waves reflecting off the top surface of a film with the waves reflecting from the bottom surface. If the thickness of the film is on the order of the wavelength of light, then colorful patterns can be obtained, as shown in the image below.
Consider the case of a thin film of oil of thickness t floating on water. For simplicity, assume that the light is incident normally, so that the angle of incidence and the angle of reflection are zero.
In the air, the light reflecting off the air-oil interface will have a 180° phase shift with respect to the incident light. A 180o phase shift is equivalent to the light having traveled a distance of 1/2 wavelength. In the oil, the light reflecting from the oil-water interface will have no phase shift with respect to the light incident on the interface. For the light reflected off the oil and the light reflected off the water to constructively interfere we need the two reflected waves to have a phase shift of an integer multiple of 2p (360o). If the light reflected off the oil-water interface travels an additional distance equal to 1/2 the wavelength of the light in oil, then the total phase shift with respect to the light reflected off the air-oil interface will be 2p. This happens if the thickness of the film is equal to 1/4 the wavelength of the light in oil. We also get constructive interference if the thickness of the film is equal to 3/4, 5/4, etc, the wavelength of the light in oil. For constructive interference we need
2t = (m+1/2)ln, m = 0,1,2,…,
where ln is the wavelength of the light in oil.
In vacuum we have lf = c. In a medium with index of refraction n we have lnf = c/n. The frequency of oscillation is the same in vacuum and in a medium, therefore
ln = l/n.
For constructive interference we therefore need
2noilt = (m+1/2)l, m = 0,1,2,….
Destructive interference occurs when the thickness of the oil film is equal to (1/2)ln, ln, (3/2)ln, etc.
For destructive interference we therefore need
2noilt = ml, m = 0,1,2,….
If the thickness of the film is (1/4)ln, the phase of the wave reflected off the top surface is shifted by p by the reflection. The phase of the wave traveling through the film is not shifted by reflection off the bottom surface, but the wave travels an extra distance of ln/2. It will therefore be in phase with the wave reflected off the top surface. If, on the other hand, the film thickness is (1/2)ln, then the wave traveling through the film travels an extra distance of 1 wavelength. It will therefore be out of phase with the wave reflected off the top surface and the two waves will cancel each other out.
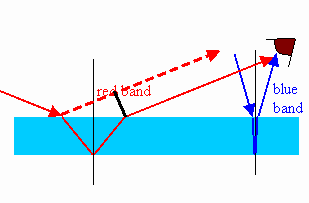
Waves incident at an angle qi on the air oil interface are refracted as they enter the oil. The angle of refraction qt is found from Snell's law, nairsinqi = noilsinqt. If they are reflected off the second interface, then they travel a distance 2t/cosqt in the oil. When they emerge again from the oil into the air and propagate parallel to the waves reflected at the air-oil interface, then the total optical path length difference is
2noilt/cosqt - 2t tanqtsinqi = 2noilt/cosqt - 2t tanqt(noil/nair)sinqt
= 2noilt/cosqt(1-sin2qt) = 2noilt cosqt.
For constructive interference we therefore need
2noiltcosqt = (m+1/2)l, m = 0,1,2,…,
and for destructive interference we need
2noiltcosqt = ml, m = 0,1,2,….
Constructive and destructive interference occur at different angles for different wavelength. The observer sees colored bands.
The destructive interference of reflected light waves is utilized to make non-reflective coatings. Such coatings are commonly found on camera lenses and binocular lenses, and often have a bluish tint. The coating is put over glass, and the coating material generally has an index of refraction less than that of glass. Then the phase shift of both reflected waves is 180°, and a film thickness equal to 1/4 of the wavelength of light in the film produces a net shift of 1/2 wavelength, resulting in cancellation. For such non-reflective coatings the minimum film thickness t required is
t = l/4n,
where n is the index of refraction of the coating material. A coating with thickness t = l/4n prevents the reflection of most of the light with a wavelength l close to l = 4nt. The coating does not reflect a specific range of wavelengths. Often that range is chosen to be in the yellow-green region of the spectrum, where the eye is most sensitive. Lenses coated for the yellow-green region reflect in the blue and red regions, giving the surface a familiar purple color.
Problems:
| When sunlight reflects from a thin film of soapy water, the film appears
multicolored, in part because destructive interference removes different
wavelengths from the light reflected at different places, depending on the
thickness of the film. As the film becomes thinner and thinner, it
looks darker and darker in reflected light, appearing black just before it
breaks. The blackness means that destructive interference removes all
wavelengths from the reflected light when the film is very thin.
Explain.
| ||
| A thin film of a material is floating on water (n = 1.33). When the
material has a refractive index of n = 1.20, the film looks bright in
reflected light as its thickness approaches zero. But when the
material has a refractive index of n = 1.45, the film looks black in
reflected light as the thickness approaches zero. Explain these
observations in terms of constructive and destructive interference and the
phase changes that occur when light waves undergo reflection.
|
The colorful patterns that you see when light reflects off a compact disk are produced by thin film interference.
A compact disc is made of a polycarbonate wafer which is coated with a metallic film, usually an aluminum alloy. The aluminum film is then covered by a plastic polycarbonate coating. The coatings are less than 100 nm thick and each coating partially reflects and partially transmits incident light. Light rays reflected from different coating boundaries interfere with each other to produce the colorful patterns. The reflectance of the CD is not uniform, because CD disk contains a long string of pits written helically on the disk. These pits encode the information stored on the CD.
Thin film interference is used in industry as a non-contact, non-destructive way to measure film thicknesses.
