Interference of non-colinear beams.

Assume a laser beam (E(r,t) = Emaxcos(k∙r - ωt) with k = 2π/λ) is split into two beams that intersect as shown in the figure below.

k1x = kcosθ, k2x = kcosθ, k1y = ksinθ, k2y = -ksinθ.
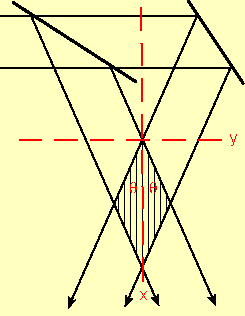
In the regions where the beams overlap we have E = E1 + E2. 
Let E = E(z/z).
E(r,t) = A1cos(k1∙r - ωt) + A2cos(k2∙r - ωt).
E(r,t)2 = (A1cos(k1∙r - ωt))2 + (A2cos(k2∙r - ωt))2 + 2A1cos(k1∙r  -ωt)A2cos(k2∙r - ωt).
cosAcosB = (1/2)[cos(A+B) + cos(A-B)]
cos(k1∙r - ωt+k2∙r - ωt) = cos(2kcosθ x - 2ωt).
cos(k1∙r - ωt - k2∙r + ωt) = cos(2ksinθ y)
E(r,t)2 = (A1cos(k1∙r - ωt))2 + (A2cos(k2∙r - ωt))2 + A1A2[cos(2kcosθ x - 2ωt)+cos(2k1sinθ y)]
<I> 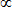<E(r,t)2>
The average values of cos2(k1∙r - ωt) and cos2(k2∙r - ωt) are 1/2, and cos(2kcosθ x - 2ωt) is zero, when averaged over a large number of periods.
<E(r,t)2> = A12/2 +A22/2 + A1A2cos(2ksinθ y)]
<I> = <I1> + <I2> + 2(<I1><I2>)1/2cos(2ksinθ y)]
The intensity therefore varies with y as C1 + C2cos(2ksinθ y) = C1 + C2cos((2π/λ')y), λ' = π/ksinθ. 
We observe fringes with fringe spacing λ'.