Properties of conductors, capacitors

Problem:

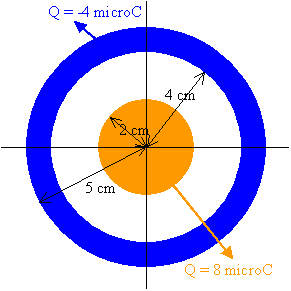
A solid conducting sphere of radius 2 cm has a charge of 8 microCoulomb.  A conducting spherical shell of inner radius 4 cm and outer radius 5 cm is concentric with the solid sphere and has a charge of -4 microCoulomb.
(a)  What is the magnitude and direction of the electric field at r = 1 cm?
(b)  What is the magnitude and direction of the electric field at r = 3 cm?
(c)  What is the magnitude and direction of the electric field at r = 4.5 cm?
(d)  What is the magnitude and direction of the electric field at r = 7 cm?

Solution:

• Concepts:
  Gauss' law, electrostatic properties of conductors
• Reasoning
  This is a problem involving charged conductors with spherical symmetry.
• Details of the calculation:
  
  (a)  The interior of a conductor is always field-free.  E = 0 inside a conductor.  The total net charge on a conductor always distributes itself over the surface of the conductor.

  (b)  The spherical symmetry of the problem tells us that the field must be radial and can only depend on the distance from the center.  The flux through a spherical surface of radius r must therefore be equal to the field times the surface area 4πr².
  Gauss' law tells us that E4πr² = Q_inside/ε₀, or E = (1/(4πε₀))Q_inside/ r^2..
  For  r = 0.03 m, Q_inside = 8*10^-6 C.  Since Q_inside is positive the field points away from the charge, radially outward.
  E = 8*10⁷ N/C radially outward.

  (c)  The interior of a conductor is always field-free.  E = 0 inside a conductor.  The total net charge on a conductor always distributes itself over the surface of the conductor.

  (d)  At r = 7 cm Q_inside is the total charge on the sphere and the shell, (8-4)microC.
  E = 7.35*10⁶ N/C radially outward

Similar problems

Problem:

A copper sphere of radius R contains a spherical cavity of radius a.  The center of the cavity is a distance d from the center of the sphere, and d and a are such that the cavity is entirely within the sphere.  There is a total charge Q on the sphere.
(a)  Find the electric field within the cavity.
(b)  Find the electric field outside the sphere.
(c)  Suppose a point charge q is placed at the center of the cavity.  What is the effect on the fields within the cavity and outside the sphere?

Solution:

• Concepts:
  Properties of conductors, shielding
• Reasoning:
  A conductor shields the fields on both sides of a closed, conducting surface from each other.  No matter how you rearrange the charges inside the cavity, the field outside the cavity will not change.  No matter what you do to the external field, the field inside the cavity will not change.
• Details of the calculation:
  (a)  The field is zero inside the cavity (shielding).
  (b)  The electric field outside the sphere is the same as that of a point charge Q located at the origin (where we placed the center of the large sphere) with no other charges present.
  (c)  The electric field outside the sphere is the same as that of a point charge Q + q located at the origin (where we placed the center of the large sphere) with no other charges present.
  The electric field inside the cavity is the same as that of a point charge q at the center of the cavity with no other charges present.

Problem:

N = 10⁶ small, conductive, and widely separated spherical droplets are merged into one spherical drop.  The radius of each droplet is r = 5.0*10^-4 cm and the electrical charge of each droplet is q = 1.6*10^-14 C.
(a)  Find the potential of the large drop.
(b)  How much work must be done by an external force to merge the droplets?

Solution:

• Concepts:
  Electrostatic potential and potential energy, properties of conductors
• Reasoning:
  The droplets and the merged drop are equipotential surfaces.  All the charge resides at the surface.  The potential of a drop of radius r' with charge q' is V = kq'/r', the same as the potential a distance r' away from a charge q'.
• Details of the calculation:
  (a)  N (4/3)πr³ = (4/3)πR³,  R = N^(1/3)r.  Nq = Q.
  The potential of the large drop is
  V = kQ/R = kN^(2/3)q/r = 9*10⁹*10⁴*1.6*10^-14/5*10^-6 V = 2.88*10⁵ V
  (b)  The work done equals the difference between the potential energy stored in the merged drop and the potential energy stored in the droplets.
  Electrostatic energy stored in a conducting sphere with radius r' and charge q'.
  U = ½q'V = ½ kq'²/r'.  (We can also use U = (ε₀/2) ∫_{all space}E² dV.)
  W = ½ kQ²/R  - ½ Nkq²/r =  ½ kN(q²/r) (N^(2/3) - 1) = 2.3*10^-3 J.

Similar problem

Problem:

Three point charges -Q are suspended inside a neutral, hollow ball in such a way that they cannot move.  The inside of the ball is then filled with a conducting liquid having a net charge -Q'.  Find the electric field everywhere inside the conducting liquid and outside of the ball.

Solution:

• Concepts:
  Properties of conductors, Gauss' law
• Reasoning:
  The inside of the conducting liquid is field-free.  Electrons redistribute themselves, leaving the point charges shielded by excess positive charges.  The excess negative charge distributes itself uniformly over the outer surface of the conducting fluid.
• Details of the calculation:
  Put the origin of the coordinate system at the center of the ball.
  In the liquid:  E = 0.
  Outside the ball:  E = (-1/(4πε₀))((3Q + Q')/r²) (r/r).

Problem:

Calculate the energy of the electrostatic interaction between a point charge q placed in the center of a spherical cavity of radius R, which was cut inside a very large grounded conductor, and the conductor.

Solution:

• Concepts:
  Electrostatic potential energy
• Reasoning:
  The electrostatic force is a conservative force.
  Work done by external force removing the conductor = change in electrostatic potential energy.
  W = U_after - U_before.
• Details of the calculation:
  We can view the energy as stored in the electric field. 
  Then U_after - U_before = (ε₀/2) ∫_R^∞4πr²dr (q/(4πε₀r²))² = q²/(8πε₀R).
  (Note: By only evaluating the difference, we avoid the problem with the field blowing up at the point charge.]
  The interaction energy between the point charge at the center of the cavity and the grounded conductor is -W = -q²/(8πε₀R).

Problem:

A sphere of radius R has volume charge density ρ = Krⁿ, for some constants K and n. The region r > R is filled with a conductor (all the way to infinity).
(a)  Find the volume charge density ρ in the region r > R, inside the conductor, and the surface charge density at r = R.
(b)  Find the electric field E everywhere, i.e. for r < R and for r > R.
(c)  Find the potential Φ everywhere, taking Φ to vanish at infinity.
(d)  How much energy is stored in this system?

Capacitors

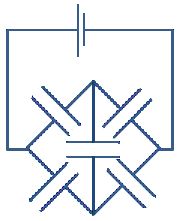
Problem:

Consider the following circuit consisting of identical capacitors with capacitance C.  What is the effective capacitance of the circuit?

Solution:

• Concepts:
  Capacitors in series and parallel, symmetry
• Reasoning:
  The central capacitor carries no charge. Thus, we can remove it (and the connectors leading to it).  This results in a circuit of two pairs of capacitors in serial arrangement that are parallel to each other.
• Details of the calculation:
  For two capacitors in series:  1/C_eff = 1/C₁ + 1/C₂.
  For two capacitors in parallel:  C_eff = C₁ + C₂.
  Since each capacitor has capacitance C, the equivalent capacitance is again C.

Problem:

A spherical capacitor consists of a spherical conducting shell of radius b and charge -Q that is concentric with a smaller conducting sphere of radius a and charge Q.  Find its capacitance.

Solution:

• Concepts:
  Gauss' law
• Reasoning:
  The problem has spherical symmetry.
• Details of the calculation:
  For a < r < b:  E(r) = kQ/r²,  ΔV = V(a) - V(b) = kQ(1/a - 1/b), 
  C = Q/ΔV = 4πε₀(ab)/(b - a).

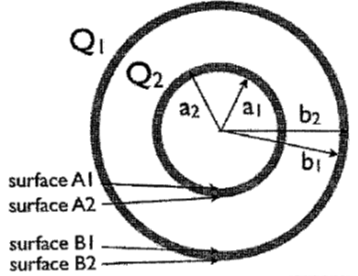
Problem:

Consider two concentric metal spheres of finite thickness in a vacuum.  The inner sphere has radii a₁ < a₂.  The outer sphere has radii b₁ < b₂.  A charge Q₂ is put on the inner sphere and a charge Q₁ is put on the outer sphere.
(a)  Find the charge density on each of the 4 surfaces.
(b)  If Q₂ = -Q₁, What is the capacitance of the system?

Solution:

• Concepts:
  Properties of conductors, Gauss' law
• Reasoning:
  The problem has spherical symmetry.  In electrostatics E = 0 inside of a conductor.
• Details of the calculation:
  (a)  Surface charge density on surface with radius a₁:  σ = 0
  Surface charge density on surface with radius a₂:  σ = Q₂/(4πa₂²)
  Surface charge density on surface with radius b₁:  σ = -Q₂/(4πb₁²)
  Surface charge density on surface with radius b₂:  σ = (Q₁ + Q₂)/(4πb_b²)
  (b)  Let Q = Q₁ = -Q₂
  a₂ < r < b₁:  E(r) = Q/(4πε₀r²), 
  ΔV = V(b₁) - V(a₂) = -∫_b1^a2 E(r)dr = Q/(4πε₀b₁) - Q/(4πε₀a₂) =[ Q/(4πε₀)][1/a₂ - 1/b₁]
  C = Q/ ΔV = (4πε₀)(b₁a₁)/(b₁ - a₂)

Problem:

Find the capacitance of two concentric spherical metal shells, with radii a and b, b > a.

Solution:

• Concepts:
  Gauss' law
• Reasoning:
  For a given charge ±Q on the shells, Gauss law yield the electric field between the shells.
• Details of the calculation:
  E is radial and has magnitude Q/(4πε₀r²) = k_eQ/r².
  Therefore |ΔV| = kQ(1/a - 1/b) = kQ(b - a)/(ab),
  C = Q/|ΔV| = 4πε₀ ab/(b - a).

Problem:

Find the change in capacitance ∆C when a metal plate of thickness t is inserted into an air-gap parallel plate capacitor of capacitance C and plate separation d > t.

Solution:

• Concepts:
  Gauss' law, properties of conductors.
• Reasoning:
  Assuming a surface charge density, Gauss' law can be used to find E and V. 
  We then can find C = Q/∆V.
• Details of the calculation:
  Before insertion:  Gauss' law for E yields EA = σA/ε₀.
  ∆V_before = Ed = σd/ε₀.  C_before = Q/∆V_before = ε₀A/d.
  After insertion:  E = σ/ε₀ in the air gap, E = 0 inside the conductor.
  ∆V_after = E(d - t) = σ(d - t)/ε₀.  C_after = Q/∆V_after = ε₀A/(d - t) = Cd/(d - t).
  ∆C = C_after - C_before = C t/(d - t).

Problem:

A series circuit consists of two capacitors, a resistor, and an ideal voltage source.  The values of V, C, and R are given.  How much ordered energy would be dissipated in the circuit if an ideal wire were added to the circuit as shown?

Solution:

• Concepts:
  The energy stored in a capacitor
• Reasoning:
  When the wire is connected the energy stored in the capacitors will change.  The battery will do work moving charges. 
  The amount of ordered energy dissipated in the process is
  E_dissipated = U_before + W_battery - U_after.
• Details of the calculation:
  Before the wire is connected, V = Q/2C + Q/C = 3Q/2C, so Q = (2/3)CV. 
  (The separated charge on each capacitor is the same.) 
  The energy stored in the capacitors is ½(Q²/C + Q²/(2C)) = ¾Q²/C = (1/3)CV².
  After the wire is connected, capacitor C is shorted out. No energy is stored in it. 
  The energy stored in capacitor 2C is ½2CV² = CV². 
  The charge on the capacitor 2C is Q' = 2CV.
  The battery has moved charge ∆Q = Q' - Q  = (4/3)CV and has done work  ∆QV = (4/3)CV². 
  E_dissipated = (1/3)CV² + (4/3)CV² - CV². 
  (2/3)CV² is converted into disordered energy.