Flux, Gauss' law

Flux

Problem:

A disk with radius r = 0.10 m is oriented with its normal unit vector n at an angle of 30^o to a uniform electric field E with magnitude 2.0*10³ N/C.
(a)  What is the electric flux through the disk?
(b)  What is the flux through the disk if it is turned so that its normal is perpendicular to E?
(c)  What is the flux through the disk if its normal is parallel to E?

Solution:

• Concepts:
  Electric flux
• Reasoning:
  The flux is given by Φ = ∫E∙dA.
• Details of the calculation:
  (a)  Since the field is constant, Φ = EAcosθ, where θ is the angle between the field and the normal, and A = πr² = π(0.1)² = 0.0314 m.  Then for θ = 30^o we obtain Φ = 54.4 Nm²/C.
  (b)  Now θ = 90^o thus Φ = 0 Nm²/C.
  (c)  Now θ = 0^o thus Φ = 63 N m²/C.

Gauss' law, spherical symmetry

Problem:

A solid conducting sphere of radius 2 cm has a charge of 8 microCoulomb.  A conducting spherical shell of inner radius 4 cm and outer radius 5 cm is concentric with the solid sphere and has a charge of -4 microCoulomb.
(a)  What is the magnitude and direction of the electric field at r = 1 cm?
(b)  What is the magnitude and direction of the electric field at r = 3 cm?
(c)  What is the magnitude and direction of the electric field at r = 4.5 cm?
(d)  What is the magnitude and direction of the electric field at r = 7 cm?

Similar problem:

Problem:

Inside a sphere of radius R and uniformly charged with the volume charge density ρ, there is a neutral spherical cavity of radius R₁ with its center a distance a from the center of the charged sphere.  If (R₁ + a) < R, find the electric field inside the cavity.

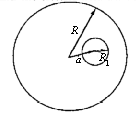
Solution:

• Concepts:
  Gauss' law, the principle of superposition
• Reasoning:
  We can view the sphere with the cavity as a superposition of a sphere with radius R having a uniform charge density ρ and another sphere with radius R₁ located in the cavity space having a uniform charge density -ρ.  The field due to each of these spherical charge distributions can be found from Gauss' law.
• Details of the calculation:
  Let the center of the large sphere be located at the origin.
  E = E₁ + E₂. 
  E₁ = ρr/3ε₀  for r < R.  
  E₂ = -ρ(r-a)/3ε₀  inside the cavity.
  Inside the cavity we therefore have E = ρr/3ε₀ - ρr/3ε₀ + ρa/3ε₀ = ρa/3ε₀  
  The field inside the cavity is constant and points into the direction of the vector a.

Problem:

The electrostatic potential V is 0 on a spherical shell of radius r₁ = 0.10 m and V is 100 Volts for a concentric shell of radius r₂ = 2.00 m.  Assume free space between these concentric shells, and find E between the shells.

Solution:

• Concepts:
  Gauss' law
• Reasoning:
  The problem has enough symmetry to find E(r) from Gauss' law alone.
• Details of the calculation:
  From Gauss' law: E(r ) ∝ 1/r² between the spheres.
  The direction of E is radially inward.  E(r) = -A/r², wit A positive. 
  Then V₀ = -∫_r1^r2E(r)dr = A∫_r1^r2(1/r²)dr = -A(1/r₂ - 1/r₁) - 100 V
  A(1/(0.1 m) - 1/(2m)) = 100 V.
  A = (100/9.5)  Vm.
  E = -10.526 V/m (r/r).

Problem:

A charge distribution produces an electric field E = A(1 - exp(-βr))(r/r³) where A and β are constants.  Find the net charge within the radius r = 1/β.

Solution:

• Concepts:
  Gauss' law
• Reasoning:
  A radial field is produced by a spherically symmetric charge distribution.
• Details of the calculation:
  E(r)4πr² = Q_inside/ε₀ in SI units.
  For r = 1/β we have A(1 - e^-1)4π = Q_inside/ε₀.
  Q_inside = A(1 - e^-1)4πε₀.

Problem:

Determine the charge distribution that will give rise to the potential V(r) = kq exp(-mr)/r, with m a positive constants.  Calculate the total charge in the distribution.

Solution:

• Concepts:
  Gauss' law, ∇²V(r) = -ρ/ε₀,
• Reasoning:
  V(r) = V(r).  ∇²V(r) = -ρ/ε₀, except at r = 0, where the expression for ∇²V(r) = is not defined.
  To find the charge at the origin we use Gauss' law.
• Details of the calculation:
  ∇²V(r) = (1/r²)(∂/∂r)(r²∂V(r)/∂r) = m² kq exp(-mr)/r = m²V(r) = -ρ/ε₀,
  except at r = 0, where the above expression for ∇²V(r) = is not defined.
  To find the charge at the origin we use Gauss' law.
  E = -∇V(r) = (∂V(r)/∂r)(r/r).  E_r(r) = (kq/r²)exp(-mr) + kq m exp(-mr)/r.
  For a spherical surface of radius r we have 4πr²E(r) = Q_inside/ε₀.
  As r --> 0, Q_inside/ε₀ = 4π kq.
  The charge distribution that gives rise to the potential V(r) = kq exp(-mr)/r therefore is
  ρ(r) = 4πε₀ kqδ(r) - ε₀m² kq exp(-mr)/r.
  With k = 1/(4πε₀ ) we have ρ(r) = qδ(r) - (m²/4π)q exp(-mr)/r.
  The total charge in the distribution is given by
  Q = ∫_{all space} ρ(r)dV = q∫_{all space} δ(r)dV - (m²/4π)q 4π ∫₀^∞ r² exp(-mr)/r dr
  = q - m²q/m² = 0.

Problem:

(a)  Consider a non-conducting sphere with radius a.  This sphere carries a net charge Q, assumed to be uniformly distributed.  Find the electric field inside and outside the sphere.  Sketch the result.
(b)  Now consider a conducting sphere with radius a carrying a net charge Q.  Find the electric field inside and outside the sphere.

Solution:

• Concepts:
  Gauss' law, Φ_e = ∫_{closed surface} E·dA = Q_inside/ε₀
• Reasoning:
  The charge distribution has spherical symmetry and E can be found from Gauss' law alone.
• Details of the calculation:
  (a)  Place the center of the sphere at the origin of the coordinate system.  Consider a spherical Gaussian surface of radius r centered at the center of the spherical charge distribution.
  i.   Let r be greater than a, so that the surface encloses the entire charge distribution. 
  The electric field is radial, the vector E is normal to any surface element dA.   Thus flux through the surface is  Φ_e = ∫ E·dA = ∫EdA = E 4πr² = Q_inside/ε₀ = Q/ε₀
  E = Q/(4πε₀r²) n, where n = r/r. 
  The field outside the sphere looks like the field of a point charge Q. 
  ii.  Let r be smaller than a, so that the surface only encloses a part of the charge distribution.  Now Q_inside is the charge density ρ = Q/V times the volume 4πr³/3 of the distribution which lies inside the spherical Gaussian surface.  We therefore have
  E = ρr/(3ε₀) n = Qr/(4πε₀a³) n.
  The field inside the sphere increases linearly with r. 
  
  (b)  The charge is uniformly distributed over the surface of the conductor.
  r >a:  E = Q/(4πε₀r²) n,  r < a:  E = 0, the electric field inside a conductor is zero in electrostatics.

Problem:

A sphere of radius R has volume charge density ρ = Krⁿ, for some constants K and n. The region r > R is filled with a conductor (all the way to infinity).
(a)  Find the volume charge density ρ in the region r > R, inside the conductor, and the surface charge density at r = R.
(b)  Find the electric field E everywhere, i.e. for r < R and for r > R.
(c)  Find the potential Φ everywhere, taking Φ to vanish at infinity.
(d)  How much energy is stored in this system?

• Concepts:
  Gauss' law, properties of conductors
• Reasoning:
  The problem has spherical symmetry.  Inside a conductor ρ and E are zero.
• Details of the calculation:
  (a)  ρ = 0 in a conductor, and since E = 0, the total charge enclosed by a Gaussian surface in a conductor is zero, so the surface charge at r = R cancels that of the charged sphere.
  σ = (1/(4πR²))∫₀⁰Krⁿ 4πr² dr = -KRⁿ⁺¹/(n + 3)
  The surface charge is uniformly distributed on the inner surface of the conductor.
  (b)  By symmetry E(r) = E(r)r/r.  Gauss' law applied to a Gaussian spherical surface of radius r < R gives
  E(r)4πr² = -4πKrⁿ⁺³/((n + 3)ε₀),  E(r) = -Krⁿ⁺¹/((n + 3)ε₀),  for r < R.
  Again E = 0 for r > R, inside the conductor.
  (c) Writing the above E as -∇Φ, we obtain
  Φ = - K(rⁿ⁺² -  Rⁿ⁺²)/((n + 2)(n + 3)ε₀) for r < 0,  Φ = 0 for r > 0.
  (d)  U = ½∫ρΦdV = (ε₀/2)∫E²dV = 2πK²R²ⁿ⁺⁵)/((2n + 5)(n + 3)²ε₀)

Problem:

Two metallic spheres of the same radius r are immersed in a homogeneous liquid with resistivity ρ.  What is the total resistance between two spheres?  Assume that the distance between two spheres is much larger than the sphere radius.

Solution:

• Concepts:
  Gauss' law, definition of I, R, and C
• Reasoning:
  Consider two conductors carrying free charges +Q and -Q respectively. 
  Consider a closed surface S surrounding the conductor carrying charge Q.
  The only excess charges inside S reside on the conductor.

  From Gauss' law:               Q = ε₀∫_SE∙n dS
  From the definition of I:     I = ∫_Sj∙n dS

• Details of the calculation:
  Using j = σE we have Q/I = RQ/V = RC = ε₀/σ.
  If the distance between two spheres is much larger than the radius of each sphere, then we have V = [1/(4πε₀)](Q/a) - (-Q/a)) = [1/(2πε₀)](Q/a)
  C = Q/V = 2πε₀a.  Therefore  R = 1/(σ2πa) =  ρ/(2πa).

Problem:

A charge Q is uniformly distributed through the volume of a sphere of radius R.  Calculate the electrostatic energy stored in the resulting electric field.

Solution:

• Concepts:
  Gauss' law, electrostatic energy
• Reasoning:
  A radial field is produced by a spherically symmetric charge distribution.
• Details of the calculation:
  From Gauss' law we have E(r) = Q/(4πε₀r²) for r > R, and E(r) = ρr/(3ε₀) for r < R. 
  Here ρ = 3Q/4πR³.  Therefore E(r) = Qr/(4πR³ε₀) for r < a.   At r = 0 we have E(r) = 0.
  The total electrostatic energy of the sphere may be calculated from the electric field, using U = (ε₀/2) ∫_{all space} E·E dV.   (SI units).
  U = (4πε₀/2)[∫₀^Rr²dr Q²r²/(4πR³ε₀)² + ∫_R^∞r²dr Q²/(4πε₀r²)²]
  = (Q²/(8πε₀))[∫₀^Rr⁴dr/R⁶ + ∫_R^∞dr /r²] = [Q²/(8πε₀)][1/(5R) + 1/R] = (3/5)Q²/(4πε₀R).

Problem:

A model of the hydrogen atom was proposed before the advent of quantum mechanics, which consists of a single electron of mass m and an immobile uniform spherical distribution of positive charge with radius R.  Assume that the positive charge interacts with the electron via the usual Coulomb interaction but otherwise does not offer any resistance to the motion of the electron.
(a)  Explain why the electron's equilibrium position is at the center of the positive charge.
(b)  Show that the electron will undergo simple harmonic motion if it is displaced a distance d < R away from the center of the positive charge.  Calculate its frequency of oscillation.
(c)  How big would the atom need to be in order to emit red light with a frequency of 4.57*10¹⁴ Hz?  Compare your answer with the radius of the hydrogen atom.
(d)  If the electron is displaced a distance d > R from the center, will it oscillate in position?  Will it undergo simple harmonic motion?  Explain!

Solution:

• Concepts:
  Gauss' law
• Reasoning:
  The field due to a spherically symmetric charge distribution can be found from Gauss' law.
• Details of the calculation:
  The charge distribution is spherically symmetric and so the electric field is  E(r) = E(r) r/r.
  Let the center of the positive charge be the origin and consider a Gaussian surface defined to be a sphere or radius r at the same origin.
  The total flux is Φ = ∫E·dA = 4πr²E(r) = Q_inside/ε₀.
  If 0 < r < R, then Q_inside = 4πρr³/3, with ρ = 3q_e/4πr³.
  In this region E(r) = ρr/(3ε₀).
  If r > R, the electric field is the same as expected for a point charge, E(r) = q_e/4π ε₀r².
  We can now easily answer the questions.
  (a)  The force acting on the electron is F(r) = -q_eρr/(3ε₀), pointing towards the origin.  Therefore the only point where the sum of all forces is zero is the origin.
  (b)  The force is a restoring force and is proportional to the displacement of the electron from r = 0.  The resulting motion will be simple harmonic motion.  
  The "spring constant" associated with this motion is k = q_eρ/(3ε₀) = q_e²/(4πε₀R³).
  The frequency of the oscillations is therefore
  f = (2π)^-1(k/m)^1/2 = (2π)^-1(q_e²/(4πε₀mR³))^1/2.
  (c)  R = [q_e²/(16π³ε₀mf²)]^1/3.  For f = 4.57*1014 Hz we need R = 3.13*10^-10 m. 
  (d)  For d > R the force is still restoring.  Therefore the electron will undergo oscillatory motion.  The magnitude of the force is proportional to 1/r², however, and therefore the motion will not be simple harmonic motion.

Problem:

A spherical charge distribution is given by
ρ = ρ₀(1 - r/a),    r < a,
ρ = 0,    r > a.
(a)  Calculate the total charge Q.
(b)  Find the electric field and potential for r > a.
(c)  Find the electric field and potential for r < a.
(d)  Find the electrostatic energy of this charge distribution.

Solution:

• Concepts:
  Gauss' law
• Reasoning:
  The field due to a spherically symmetric charge distribution can be found from Gauss' law.
• How do they apply?
  (a)  Q = 4πρ₀∫₀^a r²dr(1 - r/a) = 4πρ₀[(a³/3) - (a³/4)] = 4πρ₀a³/12.
  (b)  E = (1/(4πε₀))Q/r², radially outward for positive ρ₀.
  E = (1/ε₀)ρ₀a³/(12r²).
  Φ = (1/(4πε₀))Q/r = (1/ε₀)ρ₀a³/(12r).
  (c)  E = (1/(4πε₀)) Q_inside/r², radially outward for positive ρ₀.
  Q_inside = Q = 4πρ₀∫₀^r r'²dr'(1  -r'/a)  = 4πρ₀[(r³/3) - (r⁴/(4a))].
  E = (1/ε₀)ρ₀[(r/3)  -(r²/(4a))].
  Φ = Φ(a) + ∫_r^aE(r)dr = Φ(a) + (ρ₀/ε₀)∫_r^a[(r/3) - (r²/(4a))]dr
  = Φ(a) + (ρ₀/ε₀)[(r²/6) - (r³/(12a))]_r^a
  = (ρ₀/ε₀)[a²/12 + a²/6 - a²/12  - r²/6 + r³/(12a)]
  = (ρ₀/ε₀)[a²/6  - r²/6 + r³/(12a)].
  (d) U = (ε₀/2)∫_{all_space} E·E dV
  U = (ρ₀²/2ε₀)∫₀^a[(r²/9) - (r³/(6a)) + (r⁴/(16a²))]4πr²dr
  + (ρ₀²a⁶/288ε₀)∫_a^∞(1/r⁴)4πr²dr
  = (ρ₀²a⁵/ε₀)*0.0648.
  or
  U = (1/2)∫₀^aρ(r)Φ(r)dV = (4π/2)∫_r^aρ(r)Φ(r)r²dr
  = (2πρ₀²/ε₀)∫₀^a(1 - r/a)[a²/6  - r²/6 + r³/(12a)]r²dr
  = (ρ₀²a⁵/ε₀)*0.0648.

Similar problem

Gauss' law, cylindrical symmetry

Problem:

A 500 m length of high-voltage cable is undergoing electrical testing.  The cable consists of two coaxial conductors, the inner of 5 mm diameter and the outer of 9 mm internal diameter.  The space between the conductors is filled with polythene which has a relative permittivity of 2 and which can withstand electric field strength of 60 MVm^-1.
(a)  Find the maximum voltage which can be applied between the conductors and the energy stored in the cable at this voltage.
(b)  If the cable is to be discharged to a safe level of 50 V in 1 minute, what value of resistance must be connected across it?  What is the maximum power and the total energy dissipated in the resistance?

Solution:

• Concepts:
  Gauss' law, the cylindrical capacitor
• Reasoning:
  The problem has enough symmetry to find D(r) and E(r) from Gauss' law alone.
• Details of the calculation:
  (a)  From Gauss' law: D(r), E(r ) ∝  1/r between the cylinders.
  Let the outer cylinder be grounded and V₀ be positive.  Then the direction of E is radially outward. 
  E(r) = A/r, with A positive.  Then V₀ = -∫_b/2^a/2E(r)dr = A∫_a/2^b/2(1/r)dr
  = A(lnb/2 - lna/2) = Aln(b/a).  A = V₀/ln(b/a),
  with a = 5 mm and b = 9 mm.
  E(r) = V₀/(rln(b/a)).  
  If E_max = E(a/2) = 2V₀/(aln(b/a)) = 60 MV/m, then
  V₀ = (6*10⁷ V/m)*(2.5*10^-3 m)*ln(9/5) = 8.82*10⁴ V is the maximum voltage which can be applied.
  Energy stored in the cable: 
  W = (ε/2)∫E²dV = (εL/2)2π∫_a/2^b/2E²rdr = επL∫_a/2^b/2(V₀/(rln(b/a)))²rdr.
  W = [επLV₀²/ln(b/a)] = [2πε₀(500 m)*(8.82*10⁴ V)²/ln(9/5)] = 368 J.

Problem:

A plasma is generated inside a long hollow cylinder of radius R.  It has the charge distribution
ρ(r) = ρ₀/(1 + (r/a)²)²,
where r is the distance to the center, and ρ₀ and a are constants.
(a)  What is the electric field inside and outside the cylinder?
(b)  Setting V(r=0) = 0, find the potential at all points r < R.
(c)  What are the equilibrium positions of a particle with charge q placed inside the cylinder, assuming the charge does not alter ρ(r).  What is the force acting on the particle if it is displaced by a distance ε << a from an equilibrium position.  Are the equilibrium positions stable? 

Solution:

• Concepts:
  Gauss' law
• Reasoning:
  Choose cylindrical coordinates.  Then E will only have a radial component, E = E(r) (r/r).
• Details of the calculation:
  (a)  For a volume of unit length:  2πrE = Q_inside/ε₀.
  For r < R:  2πrE = (ρ₀/ε₀)2π∫₀^rr'dr'(1 + (r'/a)²)^-2.
  ε₀rE/ρ₀ =  ∫₀^rr'dr'(1 + (r'/a)²)^-2 = a²∫₀^r/axdx(1 + x²)^-2 = (a²/2) ∫₀^Ydy(1 + y)^-2 = -(a²/2)(1 + y)^-1|₀^Y
  with Y = (r/a)².
  ε₀rE/ρ₀ = (a²/2)(1 - 1/(1 + (r/a)²)) = (r²/2) /(1 + (r/a)²).
  For r < R:  E(r) = ρ₀r/(2ε₀(1 + (r/a)²)),    E(R) = ρ₀R/(2ε₀(1 + (R/a)²)).
  For r >R:  2πrE = (ρ₀/ε₀)2π∫₀^Rr'dr'(1 + (r'/a)²)^-2.
  For r >R:  E(r) = (ρ₀R²/r)((2ε₀(1 + (R/a)²)),  E = constant/r.

  (b)  V(r < R) = -∫₀^rE(r')dr' = -(ρ₀/(2ε₀))∫₀^rr'dr'/(1 + (r'/a)²) = -(ρ₀a²/(2ε₀))∫₀^r/axdx/(1 + x²).
  V(r < R) = -[ρ₀a²/(4ε₀)] ln((r/a)² + 1).

  (c)  All positions on the cylinder axis are equilibrium positions.  With respect to displacements along the cylinder axis these positions are neutral.  The force on the particle is zero.
  With respect to small displacements ε from equilibrium perpendicular to the axis of the cylinder the force is F = qE(r) ≈ qE(0) + q(dE/dr)|₀ε = q(dE/dr)|₀ε = qρ₀ε/(2ε₀) (r/r).
  This is a linear restoring force if q and ρ₀ have opposite signs. 
  If q and ρ₀ have opposite signs, then the equilibrium points are stable.
  If q and ρ₀ have the same sign, then the equilibrium points are unstable.

Gauss' law, planar symmetry

Problem:

Consider an infinite plane with a uniform charge density σ located at z = 0.
(a)  Using Gauss' law, find the electric field created by this plane.
(b)  Find the potential Φ(z).
(c)  Locate another plane with charge density -σ at z = d.  Find the potential Φ(z) everywhere.
What is the magnitude of the potential jump across the dipolar layer configurations of the two planes?
(d)  Find the force per unit area between the planes.

Solution:

• Concepts:
  Gauss' law, the electric potential
• Reasoning:
  We use Gauss' law to find the magnitude of the field produced by the plane.
• Details of the calculation:
  (a)  The electric field is perpendicular to the plane by symmetry. 
  
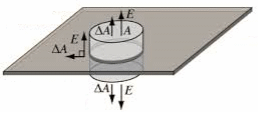
  Flux through Gaussian surface = 2E ΔA = σΔA/ε₀
  The field E produced by the sheet is E = k σ/(2ε₀) for z > 0 and  E = -k σ/(2ε₀) for z < 0.
  
  (b)  E = -k ∂Φ/ ∂z.  Let Φ = 0 at z = 0.  Then Φ = -σ|z|/(2ε₀) for all z.
  
  (c)  The potential due to the second plate is  Φ = σ|z - d|/(2ε₀) - σd/(2ε₀).
  Using the principle of superposition we have Φ_total = σ|z|/(2ε₀) + σ|z - d|/(2ε₀) + constant.
  If we want to keep Φ = 0 at z = 0, then the constant equals σd/(2ε₀).
  For z < 0:  Φ_total = -σ|z|/(2ε₀) + σ|z|/(2ε₀)  + σd/(2ε₀) - σd/(2ε₀) = 0
  For 0 < z < d:  Φ_total = -σz/(2ε₀) - σz|/(2ε₀)  + σd/(2ε₀) - σd/(2ε₀) =  - σz/ε₀.
  For z > d:  Φ_total = -σz/(2ε₀) + σz|/(2ε₀)  - σd/(2ε₀) - σd/(2ε₀) =  - σd/ε₀.
  The magnitude of the potential jump across the dipolar layer is σd/ε₀.
  (d)  For the two planes:  E = -k σ/ε₀ between the planes,  E = 0 everywhere else.
  The magnitude of the force per unit area between the plates is F/A = σ<E> = σ²/(2ε₀)
  
  Alternative approach:
  U = (ε₀/2)E² Ad = σ²/(2ε₀) Ad,  |F| = |dU/d(d)| = σ²/(2ε₀) A,  F/A = σ²/(2ε₀).

Problem:

A charge Q is placed a distance D from an infinite slab of non-conducting material with charge density ρ and thickness d.  What is the force on the charge?

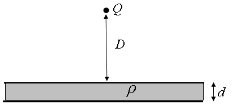
Solution:

• Concepts:
  Gauss' law, F = QE
• Reasoning:
  The problem has enough symmetry to find the electric field from Gauss' law alone.
• Details of the calculation:
  Outside the slab: E_outside = n ρd/(2ε₀), where n is a unit vector perpendicular to the closest surface and pointing away from the surface.  F_Q = n Qρd/(2ε₀).