

Let us consider a spherical interface between two media with different indices of refraction. The radius of curvature is |R|, and the center of curvature C lies on the z-axis of our coordinate system. We call the z-axis the optical axis. The vertex V is the point where the surface intersects the z-axis. R is positive if the z-coordinate of C is greater than the z-coordinate of V and negative if the z-coordinate of C is less than the z-coordinate of V.
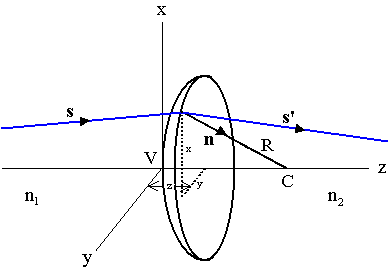
We want to trace a ray across this interface. In a medium with constant index of refraction the ray is a straight line. The equation of a line can be written as
x = x0 + tanθx(z - z0), y = y0 + tanθy(z - z0).
Here θx and θy are the angles the projections of the line in the xz- and yz-planes make with the z-axis, respectively.
We can show is that if we restrict restrict ourselves to small angles θx and θy, then the ray tracing equations for the projections of the rays on the xz-plane and on the yz-plane decouple and the projections can be treated independently. The projections behave as if the rays were actually lying in that plane. Rays that lie in a single plane containing the z-axis are called meridional rays.
Link: Mathematical details
For propagation in a single medium we have
x2 = x1 + (z2 - z1)θ1x,
θ2x = θ1x,
y2 = y1 + (z2 - z1)θ1y,
θ2y = θ1y,
and for refraction at an interface for a ray going from a medium with n1 into
a medium with n2 we have
n2θ2x =
n1θ1x - (n2 - n1)x1/R,
x2 = x1,
n2θ2y =
n1θ1y - (n2 - n1)y1/R,
y2 = y1.
The equations can be written in matrix form.
Let us concentrate on a ray in the xz-plane. We can then drop the index x on the angle, and we have
|
for refraction at an interface: |
for translation in a medium with index n: |
| n2θ2 =
n1θ1 - [(n2 - n1)/R]x1 x2 = 0*n1θ1+ x1, or
|
nθ2 =
nθ1 + 0*x1 x2 = [(z2 - z1)/n]nθ1 + x1 or
|
These transformations can be combined to give the overall transformation through several refracting and transmitting elements.
![]()
Tracing a ray across an interface
Assume a ray propagates in a medium with index of refraction n. Let the optical axis be the z axis. At any position z along this axis, a meridional ray is completely specified by giving its perpendicular distance from the axis and the angle θ it makes with the optical axis. Let us orient our coordinate system so that the ray lies in the xz-plane.
Assume a ray originates at (x1, z1) in medium 1. It makes an angle θ1 with the z-axis. We define the coordinates of the ray as
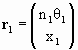 .
.
The ray propagates in medium 1 towards (x2, z2). The translation matrix T12 is given by
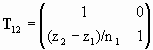 ,
,
and the ray’s new coordinates are
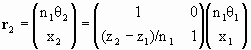 .
.
(Note that the determinant of the translation matrix T12 is 1.)
At z2 the ray encounters a spherical interface between medium 1 and medium 2 and is refracted. Its coordinates become
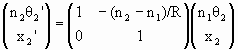
or
r2’ = Rr2 = RT12r1.
Here
(Note that the determinant of the refraction matrix R is 1.)
The ray then propagates in medium 2 towards (x3’, z3’). We have
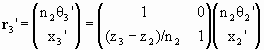
or
r3’ = T23r2’ = T23RT12r1 = Mr1.
M is the system matrix. Its determinant is 1, since det(AB) = det(A) det(B).
Matrix multiplication yields M.

![]()
Image formation
To form an image, all rays leaving the point P at (x1, z1) must arrive at the point P’ at (x3’, z3’), independent of θ1. This means that x3’ must be independent of θ1, or
 .
.
This can be rearranged to yield
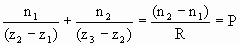 .
.
Here P is called the power of the interface.
If z1 goes to –infinity, we have
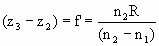 .
.
Similarly, if z3 goes to infinity, we have
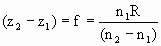 .
.
The distances f’ = n2/P and f = n1/P are called the image and object focal length, respectively.
![]()
Lateral magnification
We define the lateral magnification Mx through the equation
x3' = Mxx1.
This yields
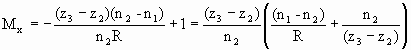 .
.
Using equation (4) we obtain
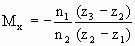 .
.