Matrices:

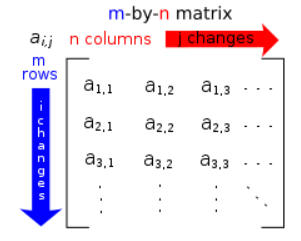
A m-by-n matrix is an array of numbers with m rows and n columns.  The individual entries in a matrix are called the matrix elements

Two matrices of the same size can be added or subtracted by adding or subtracting the corresponding elements. 
Let the elements of a matrix A be a_ij ( i = 1 - m, j = 1 - n) and the elements of a matrix B be b_ij. 
The the elements of the sum matrixC = A + B are c_ij = a_ij + b_ij and the elements of the difference matrix C = A - B are d_ij = a_ij - b_ij.

Two matrices A and B can be multiplied to produce C = AB only if number of columns of A equals the number of rows of B.
Let A be an m-by-n matrix and B be an n-by-p matrix. 
The product matrix C = AB will have m rows and p columns.

The rules for matrix multiplication are [AB]_ij = c_ij = a_i1b_1j + a_i2b_2j + a_i3b_3j + ... +a_inb_nj =  ∑_k=1ⁿ a_ikb_kj.

Example:

Writing linear equations in matrix form.

Consider the general system of m equations for n variables.

.

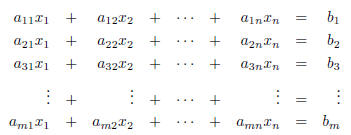We can use the rules for matrix multiplication and write the equations in matrix form.

.

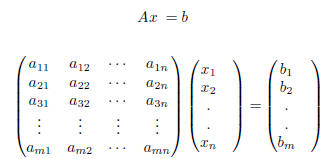The coefficient matrix for the system is

 .
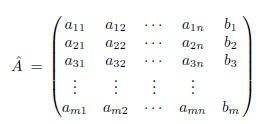