

For an optical system such as a thick lens or a compound lens, the refracting surfaces are not necessarily close together. The initial and final refracting surfaces intersect the optical axis at V and V’. The transformation matrix from V to V’ has the general form
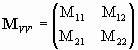 ,
det(M) = 1.
,
det(M) = 1.
We are now looking for new reference planes intersecting the optical axis at H and H’ for which the transformation matrix MHH’ will take on the form of the matrix for a thin lens.
These planes are called the principal planes of the optical system.
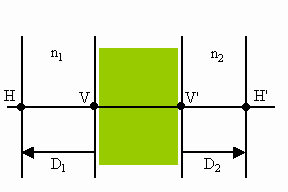
If the figure above defines D1 and D2 we have, i.e. if D1 > 0 then H is to the left of V and if D2 > 0 then H’ is to the right of V’, then
MHH’ = T’MVV’T,
where
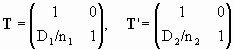 .
.
We therefore have
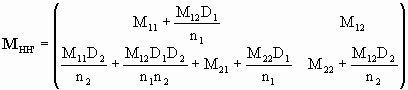 .
.
We want
 ,
,
i.e. we want it to take on the form of the matrix of a thin lens.
We therefore need
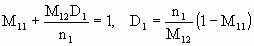 ,
,
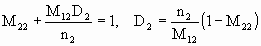 ,
,
 .
.
These equation tell us how to locate the principal planes given MVV’. They are only meaningful if M12 is not equal to zero, i.e. if we have an image-forming system. Psyst is called the overall system power.
| D1 > 0 if H is to the left of V. | |
| D2 > 0 if H’ is to the right of V’. |
has the form of a matrix connecting conjugate planes. H and H’ are therefore images of each other with unit lateral magnification. Rays undergo apparent refraction only at the principal planes. Between the principal planes, rays are mathematically translated without changing the distance from the optical axis.
Of course, the principal planes are only mathematical entities. The real refraction occurs at the physical surfaces.
For a thick lens we know the elements of MVV’.
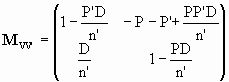 .
.
We can therefore solve for D1 and D2 and the distance t = D1 + D2 + D between the principal planes.
D1 = n1P'D/(-Psystn’), D2 = n2PD/(-Psystn’).
If n1 = n2 = 1, then
D1 = (-P’/Psyst)(D/n’), D2 = (-P/Psyst)(D/n’), t = D(1-(P+P')/(n’Psyst)).
If the lens is thin we approximately have
D1 = (-P’/(P+P'))(D/n’), D2 = (-P/(P+P'))(D/n’), t = D(1-1/n').
For a typical value of n’ = 1.5, t = D/3.
In the paraxial approximation an optical system behaves like a single lens when referred to the overall system principle planes.
![]()
Assume we have an optical system with system matrix
 .
.
What is the relationship between a general object and its image?

Let Q’ be the image of a point Q formed by some system of lenses. Q lies in the object plane C and Q’ in the image plane C’. The matrix that transforms points in the plane C into points in the Plane C’ is
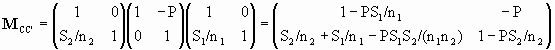
The transformation is a transformation between conjugate planes, and therefore must have the form
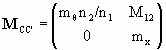 .
.
Equating the elements of the two matrices we have
| 1 - PS1/n 1= mθn2/n1, | |
| 1 - PS2/n2 = mx, | |
| S2/n2 + S1/n1 - PS1S2/(n1n2) = 0, or n1/S1 + n2/S2 = P. |
The last equation is the familiar thin lens equation. Provided S1 and S2 are measured from the principle planes, the imaging behavior of a complicate optical system in the paraxial limit is the same as that of a thin lens.