Let P’ be the image of a point P formed by some system of lenses.  P and P’ are called conjugate points and they lie in conjugate planes.

The geometry and refracting characteristics of the optical system are contained in the transformation matrix M.  If r₁ characterizes a ray entering the optical system at P and r₂ characterizes that same ray exiting the system at P’, then

.

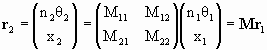Since P’ is an image of P, x₂ must be independent of θ₁.  We need M₂₁ = 0.

We then have x₂ = M₂₂x₁.  Since x₂/x₁ is the lateral magnification m_x, we have m_x = M₂₂.

For θ₂ we have

.

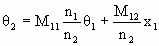For two different rays leaving x₁ and arriving at x₂ we therefore have

.

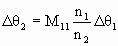If we define the ray angle magnification m_θ = Δθ₂/Δθ₁, then we have

.

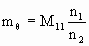Since the determinant M equals 1, M₁₁*M₂₂ = 1. 

This yields m_xm_θ(n₂/n₁) = 1, or (x₂/x₁)(Δθ₂/Δθ₁)(n₂/n₁) = 1, or n₁x₁Δθ₁ = n₂x₂Δθ₂ .

This is called the Lagrange equation, nxΔθ is known as the Lagrange invariant.

In terms of m_x and m_θ the overall transformation matrix between conjugate planes may be written as

.
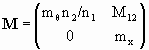