

Problem:
A glass rod of index n2 = 1.5 has a hemispherical convex surface of radius R = 6 cm on one end as in in the figure below. A ray makes an angle θ1 equal to 0.1 radians with the plane PP at a height of x1 = 1.6 cm from the optical axis. The plane PP is 8 cm to the left of the vertex V. Find the height of the ray x2 and its direction θ2 at the plane QQ 9 cm to the right of V.
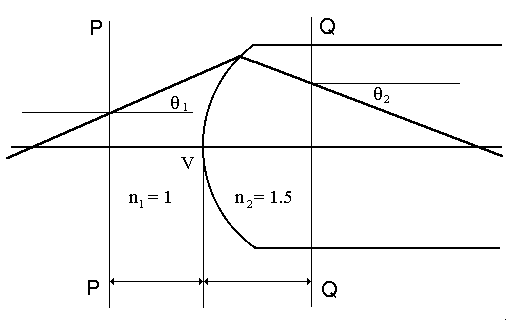
|
Solution: |

In this problem n2 = 1.5, n1 = 1, n2 - n1 = 0.5, R = 6 cm, z2 - z1 = 8 cm, z3 - z2 = 9 cm, x1 = 1.6 cm, θ1 = 0.1 radians. Therefore
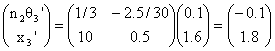 ,
,
Here all distances are measured in cm.
x3 = 1.8 cm, θ2 = -0.1/1.5 = -0.067 radians.
Problem:
Find the image and object focal length of the above system.
|
Solution: |
The image focal length is f' = n2R/(n2 -n1) = 18 cm and the object focal length is f = n1R/(n2 -n1) = 12 cm.
Problem:
For an object located 18 cm to the left of V, find the image distance.
|
Solution: |
1/18 + 1.5/(z3 - z2) = 0.5/6, (z3 - z2) = 54 cm.
We have a real image.
Problem:
For an object located 6 cm to the left of V, find the image distance.
|
Solution: |
1/6 + 1.5/(z3 - z2) = 0.5/6, (z3 - z2) = -18 cm.
We have a virtual image.
Link: Ray tracing with Excel and Matlab
Please explore and practice matrix multiplication in Excel and Matlab.