Ray tracing (single interface):
Explore ray tracing using Microsoft Excel. The linked spreadsheet traces rays across a single spherical interface in the paraxial approximation using matrix multiplication. It contains a macro, which increments the launch angle for 7 rays. The results of the calculations are plotted. The object position, the radius of the interface, and the indexes of refraction can be chosen by the user. The object position can be on either side of the interface. Please explore the spreadsheet and feel free to modify it. Here is also a simple Matlab version (right-click to download) of ray tracing across a single interface and a small file demonstrating how to do symbolic matrix multiplication in Matlab (right-click to download).
![]()
Assume you want to find the product C of two matrices, A and B.
Example 1

Type in your two matrices, one number per cell. Check your dimensions. Matrix multiplication is possible if the number of columns of A equals the number of rows of B. If A is a m x n matrix and B is a m' x n' matrix, then C will be a m x n' matrix.
Select an m x n' rage of empty cells. Do nor click anything. Start typing the formula = MMULT(. You are using the build-in Excel function =MMULT(array1,array2). You will see the formula appear in the first cell of your selected range.
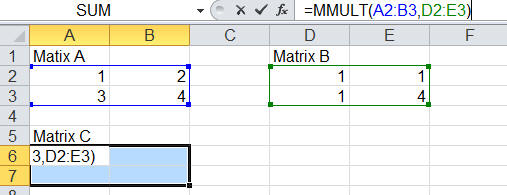
After you type the opening parenthesis, use your mouse to select the cells of matrix A. Type a comma, and then use your mouse to select the cells of matrix B. Type a closing parenthesis, but DO NOT hit Enter! Hold down CTRL+SHIFT and hit Enter. The elements of C will appear in your selected cells.

Example 2

![]()
| MATLAB is one of a few languages in which each variable
is a matrix (broadly construed) and "knows" how big it is. Moreover, the
fundamental operators (e.g. addition, multiplication) are programmed to
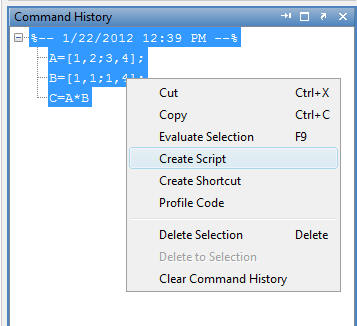
deal with matrices when required. You can initialize your matrices by simply typing them into the Command Window, as shown on the right. You can suppress intermediate output with the semicolon.
|
 |
You can also create a MATLAB script file (m-file) by
typing your commands into the editor or by converting your Command
History into a script file. |
 |
![]()
The Symbolic Math Toolbox software provides a set of tools for symbolic computing that augments the numeric capabilities of MATLAB. To declare variables as symbolic objects use the syms command. You can then manipulate the symbolic objects according to the usual rules of mathematics.
Example
%symbolic matrix multiplication
%MM = T23*RR*T12
%define the symbolic variables
syms z1 z2 z3 n1 n2 R;
%create the symbolic matrices
RR = [1, (n1-n2)/R; 0, 1]
T12 = [1, 0; (z2-z1)/n1, 1]
T23 = [1, 0; (z3-z2)/n2, 1]
%matrix multiplication
MM = T23*RR*T12
simplify(MM)
%substitute numeric values for symbols
subs(MM,{n1, n2, R},{1,1.5,-5})