

For a monochromatic plane wave in a material v = 1/(εμ)½ = c/n. The index of refraction is n = c(εμ)½. For most dielectric materials μ ~ μ0, and n = (ε/ε0)½ .
What determines the permittivity ε for a material?
For a linear, isotropic, homogeneous material we have
P = ε0χeE, D = ε0E + P = ε0 (1 + χe)E = εE.
So the permittivity ε is determined by how easily a material can be polarized.
![]()
Anisotropic materials:
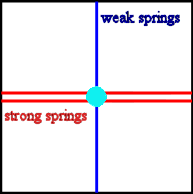
Assume that in a material the electron moves in a potential that has a local minimum and that near this minimum can be modeled as a anisotropic harmonic oscillator potential. In a simple model in two dimensions, we may picture the electron in a square box, connected by strong springs to the right and left walls and by weak springs to the top and bottom walls.
|
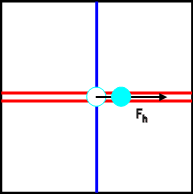
Let a force of
magnitude Fh = F' pointing towards the right produce a
displacement of magnitude d and a dipole moment of magnitude -qed. |
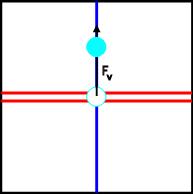
Let a force of magnitude Fv = F' pointing upwards produce a displacement of magnitude 2d and a dipole moment of magnitude -2qed. |
|
|---|---|---|
 |
 |
 |
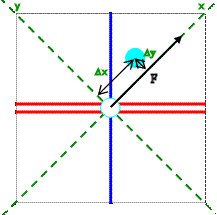
If we choose the coordinate system shown in the figure below, and apply a force F = Fh + Fv in the x-direction, then this force produces a displacement Δx = 3d/√2 in the x-direction and a displacement Δy = d/√2 in the y-direction. The dipole moment and the polarization therefore have a x- and a y-component. If the force F is due to an electric field E, then P and E are not parallel vectors.
The electromagnetic wave produced by the oscillation dipoles can be viewed as a superposition of two waves, polarized along the two different symmetry axes. These two component propagate with different speed c/n, because the index of refraction is different for the different components. The angle of refraction depends on n, so the angle of refraction will be different for the different components.