When an electromagnetic wave propagates through a material, the particles of the medium are displaced from their equilibrium positions.  Positively charged particles move in the direction of the field, while negatively charged particles move in the direction opposite to the direction of the electric field.  This relative displacement of positively and negatively charged particles creates dipole moments.  The dipole moment per unit volume describes the induced polarization P of the medium.

In a linear material the relative displacement of positively and negatively charged particles is proportional to the instantaneous magnitude of the electric field.  But all real materials, when exposed to a high enough light intensity show a nonlinear response.  In return the medium modifies the electromagnetic field in a nonlinear way. 

When the magnitude of the external field is small, the magnitude of the electric polarization is approximately linearly proportional to the electric field E.  In an isotropic material we write

P = ε₀χ_eE.

In an anisotropic material P and E can have a different direction.

When the magnitude of external electric field is large, the induced polarization has a nonlinear dependence on the electric field and can be expressed as a power series with respect to the electric field.  In an isotropic material we have

P = ∑_nε₀χ⁽ⁿ⁾Eⁿ.

In an anisotropic material P and Eⁿ can have a different direction.

χ⁽¹⁾ is the linear susceptibility linear absorption and refraction.  χ⁽²⁾ is the first non-linear term.  It only is nonzero in anisotropic materials.  χ⁽³⁾ is the second non-linear term, which can be nonzero in all materials.

Electric fields associated with light from ordinary non-coherent sources are usually too small to trigger an observable nonlinear response.  But the magnitude of electric fields from pulsed laser beams focused onto a small spot can approach the magnitude of typical internal fields in crystals.  In general it takes fields greater than of 10⁵ V/m to observe nonlinear optical phenomena.  These optical fields are easily generated by lasers.  Equally important, the coherence of the laser light makes it possible to observe many nonlinear phenomena.  When the molecules in the material respond coherently to the laser light, even the weakest nonlinear effects can be detected.

Assume E is proportional to cos(ωt).  Then P is is proportional to cos(ωt) in a linear material.  All charges oscillate with angular frequency ω and produce electromagnetic wave with angular frequency ω.  In nonlinear materials P also contains non-negligible terms that are proportional to E² and therefore to cos²(ωt) = (1/2)(1 + cos(2ωt)), and maybe terms proportional to E³ and therefore to cos³(ωt) = (1/4)(cos(3ωt) + 3cos(ωt)).  The displacement of the charges is a superposition of a constant displacement and oscillations with angular frequencies ω,  2ω, and maybe 3ω.  The material generates EM wave with twice or tree times the frequency of the incident light and also a constant electric field.

What are possible consequences?

The nonlinear index of refraction is defined as a variation of the index of refraction of the material proportional to the intensity of the light propagating through the medium.  Let us consider an optical wave propagating through an isotropic material with inversion symmetry (χ⁽²⁾ = 0).  The linear susceptibility χ⁽¹⁾ is related to the ordinary index of refraction in the linear regime.

n₀ = (1 + χ⁽¹⁾)^½ .

In the nonlinear regime the magnitude of the polarization can be expressed as:

P = ε₀ (χ⁽¹⁾E + χ⁽³⁾ E³).

This yields

D = ε₀E + P = ε₀(1 + χ⁽¹⁾ + χ⁽³⁾ E²)E = εE.

The index of refraction is

n = (ε/ε₀)^½ = (1 + χ⁽¹⁾ + χ⁽³⁾ E²)^½  ~ n₀(1 + (χ⁽³⁾ E²)/2n₀²) = n₀ + n₂I,

where I is the intensity of the optical wave, I E², and n₂ represents the nonlinear index of refraction, which depends on the intensity of the applied field.

The nonlinear index of refraction is responsible for self-focusing and soliton propagation in fibers. 

The electro-optic effect is a nonlinear effect that mixes a static field with the field of and electromagnetic wave.  If an isotropic dielectric is placed in an electric field E and a beam of light is passed through the sample perpendicular to the field then the material displays induced birefringence proportional to E².  The ordinary and the extraordinary ray propagate in the same direction perpendicular to E, but the index of refraction is different for the ordinary and extraordinary ray.  Δn = n_o - n_e = λKE², where K is the Kerr coefficient.  The Kerr effect is a third order effect, and it is sometimes referred to as the quadratic electro-optic effect.  It can be generated in materials with any molecular orientation.  It can be used to construct wave plates. 

Certain crystals exhibit a linear electro-optic effect.  Birefringence occurs when the material is placed in an electric field E and a beam of light passes through the material parallel to the field.  The ordinary and the extraordinary ray propagate in the same direction parallel to E, but the index of refraction is different for the ordinary and extraordinary ray.  The induced birefringence is proportional to E.  Δn = n₀K_pE where K_p is the Pockels coefficient, and n₀ is the index of refraction of the material with no field applied.  The linear electro-optic effect (LEO) or Pockels effect is a 2nd-order nonlinear effect.  It does not occur in isotropic media or media with inversion symmetry.  The Pockels effect can also be used to construct wave plates.

Both the Pockels and the Kerr effects can be used to construct very fast optical shutters (10^-10 s) by placing the material between crossed polarizers.  When the retardation is λ/2, the  device will be transparent.  Pockels cells typically require 5 to 10 times lower voltages than equivalent Kerr cells. 

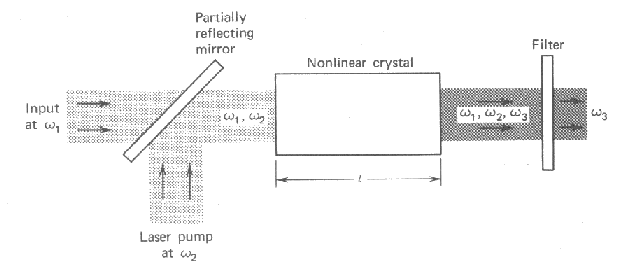
Second harmonic generation is a second order nonlinear process (ω  + ω --> 2ω).  Parametric up-conversion in a crystal can be used to convert a signal from a low frequency ω₁ to a high frequency ω₃ by mixing it with a strong laser beam of frequency ω₂ (ω₁  + ω₂ --> ω₃).  Parametric amplification involves an input signal at at ω₁ together with an intense pump beam at ω₂, ω₂ > ω₁. A photon of the pump beam with frequency ω₂ interacts with a photon with frequency ω₁ and splits into two photons, one with frequency (ω₂  - ω₁) and one with frequency ω₁. The coupling is provided by the non-linearity of the crystal.  The wave at ω₁ is amplified.  This is accompanied by the generation of an idler beam at ω₃ = ω₂  - ω₁.  The idler beam then interacts with the pump beam to produce additional amounts of signal and idler light.  A photon of the pump beam with frequency ω₂ interacts with a photon of frequency ω₃ = ω₂  - ω₁ and splits into two photons, one with frequency ω₂  - ω₃ = ω₁ and one with frequency ω₃.

In most materials the index of refraction depends on the wavelength of the EM wave,  EM waves with different angular frequencies ω propagate with slightly different speeds.  Consider, for example, second harmonic generation.  Light with frequency 2ω generated at some point P₁ in the medium will not be in phase with light with frequency 2ω generated at some other point P_2.  As a result, the two waves from P₁and P₂ will interfere destructively at some point P₃.  The problem of destructive interference can be overcome by letting the fundamental be the ordinary ray and the second harmonic be the extraordinary ray in an anisotropic crystal.  When the direction of propagation of the fundamental is chosen so that the index of refraction of the fundamental and second harmonic are the same, both waves will stay in phase.  The crystal then is said to be phase-matched or index-matched.  Phase matching can also be achieved in some crystals by varying their temperature.  The extraordinary index is in general more temperature-dependent than the ordinary index.  By varying the temperature one can adjust the birefringence of the crystal until phase matching is obtained.

Other Induced Optical effects

Photo-elasticity
An isotropic material can become birefringent when placed under stress.  Under compression it becomes a negative uniaxial crystal and under tension it becomes a positive uniaxial crystal.  The direction of the stress defines the direction of the optical axis.  The induced birefringence is proportional to the stress.  Photo-elasticity can be used to study stress patterns in complex objects, for example bridges, by building a transparent scale model of the object. 

Faraday Rotation in solids
If an isotropic dielectric is placed in a magnetic field B and a beam of linearly polarized light is passed through the sample in the direction of the field then a rotation of the plane of polarization will occur.  The angle θ through which the direction of polarization is rotated is proportional to B and the thickness of the material.  The proportionality constant is called the Verdet constant.  The direction of the rotation depends on whether light is traveling parallel or anti-parallel to B.