

| Let us look at a mathematical description
of polarization. The electric field of any polarized beam propagating
along the z-axis may be written as E = Exi + Eyj ,
where Ex = Axexp(i(kz - ωt)), Ey = Ayexp(i(kz - ωt + φ)). We can write the components as a column vector, which is called a Jones vector. |
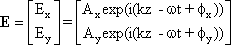 |
| We may factor out and the dependence on z and t and just write the expression on the right. The intensity of the beam is proportional to Ax2 + Ay2. The most general Jones vector of a polarized beam propagating along the z-axis is given by this equation. |
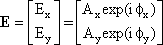 |
| The Jones vector for horizontally polarized light: |
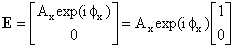 |
| The Jones vector for vertically polarized light: |
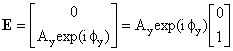 |
| The normalized Jones vector for light polarized at 45o, where Ax = Ay = A = 1 and
φx
= φy = φ =
π/4. (Normalization means that Ex2 + Ey2 = E2 = 1.) |
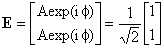 |
| The normalized Jones vector for right-hand circularly polarized light: |
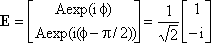 |
For the normalized vectors we have
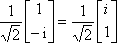 . .
|
|
| If a polarized beam with field vector E is incident on a
polarization-changing medium such as a polarizer or a wave plate, then the result
is a beam in another polarization state given by E' with E'x =
m11Ex + m12Ey, E'y = m21Ex
+ m22Ey. We write: The 2 by 2 transformation matrix is called the Jones matrix. The table below lists the Jones matrices for common optical elements. |
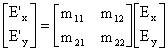 |
| Optical Element | Jones matrix |
| horizontal linear polarizer |
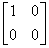 |
| vertical linear polarizer |
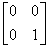 |
| linear polarizer at θ |
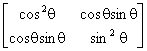 |
| quarter wave plate (fast axis vertical) |
 |
| quarter wave plate (fast axis horizontal) |
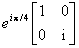 |
| If we require the Jones matrix for an optical element which has been rotated through an angle θ with respect to the direction given in the table above, we must multiply the above matrix by the usual matrices for rotation. |
M(θ) = R(θ) M R(-θ), where
|
To find the Jones matrix for a sequence of polarization transformations, for example a linear polarizer followed by a quarter wave plate, we simply multiply the individual Jones matrices together in the correct order. If an incident beam of light with field vector E passes through a sequence of four polarizing elements, M1 followed by M2, M3 and M4, then the resultant field vector E' is given by
E' = M4 M3 M2 M1 E.
The eigenvectors of the Jones matrix M of an optical device correspond to the polarization states which propagate through the optical device represented by M unchanged. The beam enters and emerges in the same polarization state. The eigenvalues, which in general are complex numbers, tell us about changes in amplitude and phase produced by the optical device.
Link: The Jones Calculus.