

Geometrical optics in the paraxial approximation predicts that the image of a point produced by an image-forming optical system is a point. But the image of a point produced by a real optical system is not a point but a small, blurred spot. This is due to diffraction and various forms of aberrations. The blurred-spot image of a single point is called the point-spread function or the impulse response of the optical system.
If the object is illuminated with coherent light, then the impulse response is the amplitude image of a point source. If the object is illuminated with incoherent light, then the impulse response is the intensity image of a point source.
Systems are called shift invariant, if the impulse response does not depend on the position of the point source in a plane perpendicular to the optical axis. If a system is shift invariant, and we move a point perpendicular to the optical axis, the blurred image spot moves, but its shape stays the same. Real system can only be approximately shift invariant.
![]()
Assume we have a shift invariant optical system and let the impulse response the system be T(x'). (We restrict ourselves to one dimension.) Assume an extended object is illuminated incoherently. The intensity distribution in the object plane is I(x). What is the intensity distribution I'(x') in the image plane?
Geometrical optics in the paraxial approximation predicts a distribution Ig(x'), which has the same functional form as I(x), but is scaled to take into account the magnification of the optical system. But because the image of each point of the extended object is blurred by the impulse response, all points x of the object contribute to the image at x'. I'(x') must be expressed as an integral over the entire I(x) plane. Since Ig(x') is a scaled I(x), we can also integrate over the entire geometrical optics image plane.

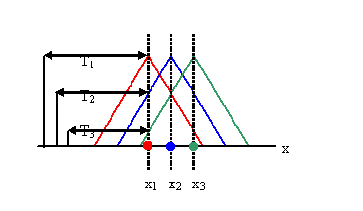
| [Assume you have three discrete point sources and that
geometrical optics predicts an intensity Ig for the image of each
source. The image of each source is smeared by a triangular impulse response, as
shown in the figure below. At position x1 we now observe I(x1) = Ig(x1)T1
+ Ig(x2)T2 + Ig(x3)T3
|
 |
The image intensity is the convolution of the object intensity and the impulse response of the system. We write
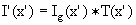 ,
,
where the special symbol denotes the convolution of Ig(x') and T(x').
If the object is illuminated with coherent light we rewrite the above equation in terms of field amplitudes instead of intensities.
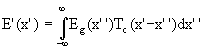
Here Tc is the coherent impulse response.
A convolution is an integral which expresses the amount of overlap of one function g as it is shifted over another function f. It "blends" one function with another.f(x')*g(x') = ∫-∞+∞f(x'')g(x'-x'')dx'' = ∫-∞+∞g(x'')f(x'-x'')dx''
A graphical representation of a convolution is shown below. Here f (object) and g (response) are both rectangular functions. The function f is a function of x'', where x'' is the horizontal coordinate. The function g is a function of x'-x'', and x' changes from frame to frame. The convolution measures the overlap of the two functions f and g as a function of x'.]

Download the linked spreadsheet convolution.xlsm to explore the convolution of various functions represented as the overlap of the two functions as one is shifted over the other.
Link:
| Convolution |
Convolution Theorem
The Fourier transform of the image predicted by geometrical optics Ig(x') is Ig(k).
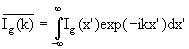
Here we incorporate the factor (2π)-1/2 into Ig(k).
The Fourier transform of the impulse response T(x') is T(k).
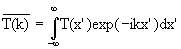
T(k) is called the optical transfer function (OTF). The optical transfer function is the Fourier transform of the impulse response.
Let us find the Fourier I'(k) of I'(x) i.e. the Fourier transform of the actual image.
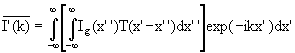 .
.
Reversing the order of integration we have
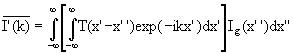 .
.
Defining α = x' - x'' we write
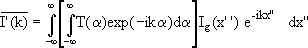 .
.
But
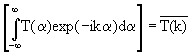 .
.
We therefore write
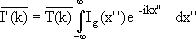
or I'(k) = Ig(k) T(k).
This is the convolution theorem. The Fourier transform of a convolution is the product of the Fourier transforms of the component functions.
|
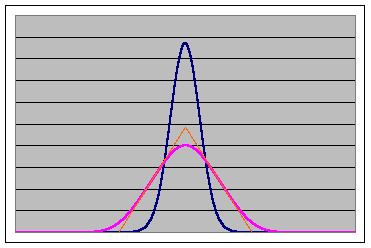
The figure on the right shows a Gaussian object intensity (blue) convoluted with a triangular impulse response (orange) to produce the image intensity (pink). This convolution was performed by multiplying the Fourier transforms of the Gaussian and the triangle and then calculating the inverse transform using Excel. Click on the llnk to examine the spreadsheet convolutionFFT.xlsm. [In this spreadsheet the response function is normalized. You can pick different object functions and different response functions. The input range for the spreadsheet contains 1024 values. Since Excel's Fourier transform tool assumes periodic data starting at x = 0, the data corresponding to the negative x-values are in the second half of the range.] The convolution theorem suggest a method of recovering Ig(x') from I'(x') if the point spread function can be determined. We calculate the Fourier transforms I'(k) of I'(x') and T(k) of T(x') and then calculate Ig(k) = I'(k)/T(k). The inverse Fourier transform yields Ig(x'). However, this process is very sensitive to error and noise. |
 |
A MATLAB example script convoluting an image with a point spread bunction using the convolution theorem is linked here. Download your MATLAB directory and run.
| Fourierconv.m |
![]()
To get a feel for which features remain recognizable and which get washed out given a certain impulse response, let us consider an object intensity that varies sinusoidally with x, and let Ig(x') = exp(-ik'x') describe this intensity. The Fourier transform of exp(-ik'x') is the Dirac delta function δ(k'-k). [The object contains only a single spatial frequency.]
exp(-ik'x') = ∫δ(k'-k)exp(-ikx')dk.
We therefore have I'(k) = Ig(k) T(k) = δ(k'-k) T(k). To find I'(x') we use
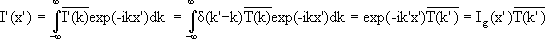 .
.
For a sinusoidally varying object intensity, the image intensity is equal to the object intensity multiplied by the optical transfer function T(k'). T(k) is the Fourier transform of the point spread function, it tells us the spatial frequency content of the point spread function. For example, if the point spread function is a Gaussian function, then T(k) is a Gaussian function centered at k = 0. The optical transfer function, T(k'), is proportional to the ratio of the image intensity of a sinusoidal grating with spatial frequency k' to the object intensity of the grating. For any reasonable transfer function the magnitude of T(k') decreases rapidly as k' becomes very large.
The magnitude of the optical transfer function is called the modulation transfer function (MTF). The phase of the OTF is in general not zero, and a nonzero phase indicates a shift in the pattern from the position predicted by geometrical optics.
The MTF is a measure of the contrast of an optical image at a specified spatial frequency k'. At high spatial frequencies (high values of k') the MTF (magnitude of the Fourier transform) becomes very small or zero.
![]()
The same reasoning we use for the incoherent case we can use for the coherent case. For the coherent case we replace the intensities I(x), Ig(x') and I'(x') with field amplitudes E(x), Eg(x') and E'(x'), and we replace T(x') and T(k) with Tc(x') and Tc(k).