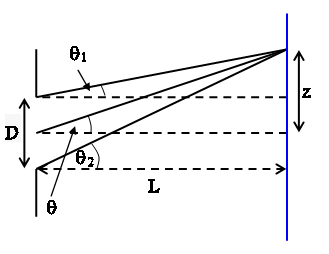

Consider a slit of width D. In the Fraunhofer approximation the first
diffraction minimum appears on a screen a distance L from the slit when Dsinθ =
λ or Dz/(L2
+ z2)1/2 = λ. Then the difference in the lengths of the lines making angles
θ2 and θ1
with the normal in the figure above is λ.
Using geometry we have
(L2 + (z + D/2)2)1/2 - (L2 + (z -
D/2)2)1/2 = λ.
(L2 + z2 + zD + (D/2)2)1/2 - (L2
+ z2 - zD + (D/2)2)1/2 =
λ.
(L2 + z2)1/2(1 + ((D/2)2 + zD)/(L2
+ z2))1/2 - (1 + ((D/2)2 - zD)/(L2 +
z2))1/2 = λ.
With L >> z and D we can expand the square root.
(L2 + z2)1/2(1 + (1/2)((D/2)2 +zD)/(L2
+ z2)) - (1 + (1/2)((D/2)2 - zD)/(L2 + z2))
= λ.
Dz/(L2 + z2)1/2 = λ.
Since L >> z, we have Dz/L = λ.
For the Fraunhofer approximation to be valid we need L >> z and D.
But to be able to resolve the minimum. On the screen we want the central maximum and the first diffraction minimum
to be well separated. We want to avoid destructive interference of spherical
wavelets emanating from different points of the slit. We therefore need (L2
+ D2)1/2 - L << λ/2. With
L >> z and D this yields
L(1 + (1/2)D2/L2) - L << λ/2, or
D2 << λL.