Diffraction

The single slit

Recall:  Dark fringes in the diffraction pattern of a single slit are found at angles θ for which

w sinθ = mλ,

where m is an integer, m = 1, 2, 3, ...  .

Details:

Assume light from a distant source passes through a narrow slit as shown on the figure on the right.  Assume the incident wave can be treated as a plane wave E(r,t) = k Ecos(kx - ωt + φ).  The polarization of this wave perpendicular to the plane of the figure.  Let the slit  be very long. L et us concentrate on the region near the middle of the slit and neglect variations of the transmitted wave perpendicular to the plane of the figure.  (We are reducing the problem from a 3D to a 2D problem.)  What do we observe on a distant screen?

 
According to the Huygens-Fresnel principle, the total field at a point y = d*tanθ on a screen a large distance d from the slit is the superposition of radiation fields from an infinite number of point sources in the aperture region.  Each section on the wave front between s and s + ds inside the aperture (-a/2 ≤ s ≤ a/2) is the source of a spherical wave.  A large distance r from the point source between s and s + ds the radiation field is due to the sources is

dE = (Asds/r)cos(kr - ωt).

Here Asds/r the field at a distance r from the point source of infinitesimally small width ds.

 

If r0 is the distance from the point s = 0 on the optical axis to a point y on the screen, then the contribution dE to the total amplitude on the screen from the point at s = 0 is
dE(y = d*tanθ) = (Asds/r0)cos(kr0 - ωt).
For off-axis points for which s ≠ 0, the distance to the screen is longer or shorter than r0 by an amount Δ.

The contribution dE(y) to the total amplitude on the screen from an off-axis point (s ≠ 0) is

dE(y) = (Asds/(r0 + Δ(s))) cos(k(r0 + Δ(s)) - ωt).

To find the total amplitude E(y) we have to add up the contributions from all points on the aperture.  Because there are an infinite number of points, the sum becomes an integral.

E(y) = ∫-a/2+a/2(A/(r0 + Δ(s)))cos(k(r0 + Δ(s)) - ωt)ds.

We define sinθ = Δ/s.  Since r0 >> Δ, we approximate 1/(r0 + Δ) with 1/r0.  However we cannot drop the Δ inside the cosine function, since kΔ(s) is not necessarily much smaller than 2π.  We then have

E(y) = (As/r0)∫-a/2+a/2cos[(ksinθ)s + (kr0 - ωt)]ds.

Using ∫cos(ax + b)dx = (1/a)sin(ax +b) the integration yields

E(y) = (Asa/r0)cos(kr0 - ωt)(sin(ka(sinθ)/2)/(ka(sinθ)/2).

or, inserting k = 2π/λ,

E(y) = (Asa/r0)cos(kr0 - ωt)(sin(πa(sinθ)/λ)/(πa(sinθ)/λ).

 
The function sin(x)/x = sinc(x) is called the sinc function.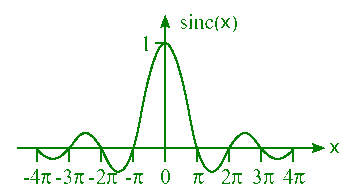
The intensity is proportional to the square of the field,  I(y) E2(y).  Since the square of a cosine function averages to ½, the time-averaged intensity is given by

<I(y)> = <I0>sin2(πa(sinθ)/λ)/(πa(sinθ)/λ)2,

where <I0> is the average intensity at the center.

The time-averaged intensity has a peak in the center with smaller fringes on the sides.  For small angles we may approximate sinθ ~ θ.  Then the first zeros on the sides of the central peak occur when πasinθ/λ ~ πaθ/λ = π, or θ = λ/a.
On the screen we see a pattern similar to that shown in the figure on the right.

horizontal rule

Diffraction of light through a rectangular aperture is a rather straightforward extension of 1-dimensional diffraction from a slit, as shown in the diagram on the right.

A circular aperture is qualitatively similar, but an accurate quantitative treatment of the pattern requires more complicated mathematics.  The intensity pattern is called the "Airy Disk".  The main features are shown in the diagram on the right.  The first minimum occurs at an angle θ = 1.22λ/D, where D is the diameter of the aperture.  On a screen a distance L >> D from the aperture the minimum is seen at a radial distance r' = 1.22λL/D from the center of the pattern.

Producing a laser beam is an attempt to confine the light in the directions transverse to the direction of propagation.  The light will spread out in the same way it does after passing through an aperture.

The angle through which the light spreads is approximately θ ≈ λ/a(0).  Therefore a(z)/2 ≈ z/θ.  Because the laser beam diameter is typically much larger the wavelength of light, or a(0) >> λ, θ is quite small.  Consider a HeNe laser, for which λ = 633 nm with a beam waist of ~ 0.6 mm.  Then θ ~ 10-3 rad = 1 millirad.  The beam must propagate ~ 3 m before the diameter increases by a factor of 10.

In geometrical optics we assume that an ideal, aberration-free lens focuses parallel rays to a single point one focal length away from the lens.  But the lens itself acts like an aperture with diameter D for the incident light.  The light passing through the lens therefore spread out.  This yields a blurred spot at the focal point.  Light near the focal point exhibits an Airy Disc pattern.  The size of the Airy Disc is determined by the focal length f and diameter D of the lens.  Since the spreading angle is θ ~ r/f, the radius r of the Airy Disc at the focal point of a lens is given by r = 1.22λf/D.

If all ray aberrations in an optical system can be eliminated, such that all of the rays leaving a given object point land inside of the Airy Disc associated with the corresponding image point, then we have a diffraction-limited optical system.  This is the absolute best we can do for an optical system that has lenses with finite diameters.

The resolving power of an optical instrument is its ability to separate the images of two objects, which are close together.  Some binary stars in the sky look like one single star when viewed with the naked eye, but the images of the two stars are clearly resolved when viewed with a telescope.

Why?
The merging of the images in the eye is caused by diffraction.

If you look at a far-away object, then the image of the object will form a diffraction pattern on your retina.  For two far-away objects, separated by a small angle θ, the diffraction patterns will overlap.  You are able to resolve the two objects as long as the central maxima of the two diffraction patterns do not overlap.  The two images are just resolved when one central maximum falls onto the first minimum of the other diffraction pattern.  This is known as the Rayleigh criterion.  If the two central maxima overlap the two objects look like one.

The width of the central maximum in a diffraction pattern depends on the size of the aperture, (i.e. the size of the slit).  The aperture of your eye is your pupil.  A telescope has a much larger aperture, and therefore has a greater resolving power.  The minimum angular separation of two objects which can just be resolved is given by θmin=1.22λ/D, where D is the diameter of the aperture.  The factor of 1.22 applies to circular apertures like the pupil of your eye or the apertures in telescopes and cameras.

The closer you are to two objects, the greater is the angular separation between them.  Up close, two objects are easily resolved.  As your distance from the objects increases, their images become less well resolved and eventually merge into one image.

Problem:

A spy satellite travels at a distance of 50 km above Earth's surface.  How large must the lens be so that it can resolve objects with a size of 2 mm and thus read a newspaper?  Assume the light has a wavelength of 400 nm.

bulletSolution:

Diffraction limits the resolution according to θ = 1.22λ/D = y/L.  Here the height of the object to be resolved is y and the distance to the object is L.  Solving for D we find D = 12.2 m.

Links:

bullet Airy Pattern Basics
bullet Airy Pattern Formation
bullet Light Diffraction Through a Periodic Grating
bullet Airy Patterns and the Rayleigh Criterion
bullet Numerical Aperture and Image Resolution
bulletMathematica Examples