Radiometry and Photometry

An important part of the design of an optical system is its efficiency in transferring light. One must be able to specify the amount of energy emitted or received. For historical reasons, many similar quantities are used to specify the amount of light leaving the source or arriving at the receiver, and many different systems of units are used. Only in recent years has the situation improved with the gradual changeover to the International System of Units (SI).

To specify the amount of energy emitted by a source, we use the quantities.

	Energy
	Power
	Power per unit area
	Power per unit solid angle
	Power per unit solid angle per unit projected area

To specify the amount of energy received by a detector, we use one quantity.

Power per unit area

A radian is the angle subtended at the center of a circle of radius r by a section of its circumference of length equal to r. Dividing 2πr by r gives 2π as the number of radians in a full circle.

A steradian is the solid angle subtended at the center of a sphere of radius r by a section of its surface area of magnitude equal to r². Since the surface area is 4πr², there are 4π steradians surrounding a point in space.

Let a cone of arbitrary shape have its apex at the center of a sphere of unit radius. The solid angle Ω at the apex is numerically equal to the surface area on the sphere intercepted by the cone, since the full sphere has an area of 4π.

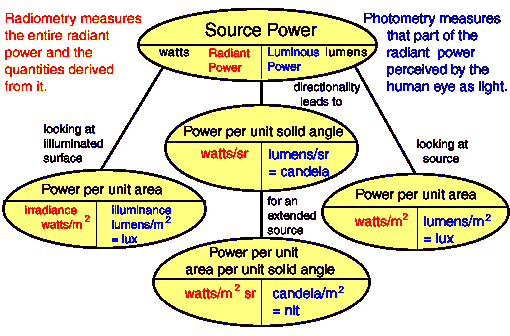
When specifying energy, power, power per unit area, power per unit solid angle, and power per unit solid angle per unit projected area, we can specify radiometric quantities, which apply to radiation of any wavelength, or photometric quantities, which only apply to visible light.

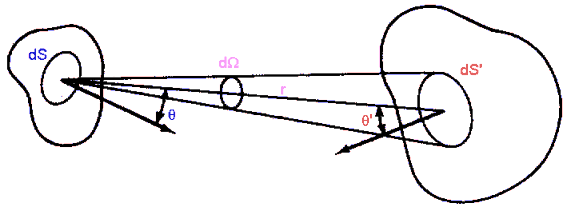
In the figure above, let the area dS be the source of electromagnetic radiation. The area dS emits radiation toward a receiving area dS’ at a distance r.

Radiometric quantities

	In SI units, the energy E of the emitted radiation is measured in Joule (J).
	The radiometric power P = dE/dt = Φ emitted from a surface dS is called the radiant flux, and it is measured in J/s = Watt (W).
	The power per unit area dP/dS = M is called the radiant emittance. It is measured in W/m².
	The power per unit solid angle dP/dΩ = I is called the radiant intensity. It is measured in unit of W/sr. It can have an angular dependence. We then specify I(θ).
	The power per unit solid angle per unit projected area is called the radiance L. It is measured in W/sr/m². An important part of the definition of L is the specification of the area. We use the normal or projected area dS cosθ, since the energy received at dS’ depends not only on the size of dS but also on its orientation. (The area is projected onto a plane whose normal is the line of sight.) L = I/(dS cosθ) = d²P/(dΩ dS cosθ)
	The amount of energy received from a source by the surface dS’ is the irradiance E, measured in W/m².

Photometric quantities

The corresponding photometric quantities are tied to the sensitivity of the human eye, our main detector for visible light.

In SI units, the energy of the emitted radiation is measured in Joule. However, if the wavelength of the emitted radiation lies in the 400—700 nm range, i.e. the visible range, then the energy is called luminous energy and its unit is the Talbot.

	The photometric equivalent of the radiant flux Φ is the luminous flux Φ, whose units are lumens (lm). The figure above shows the sensitivity of the eye as a function of wavelength or color. The peak is in the green at 555 nm. 1 W of green light is equivalent to 683 lm.
	The photometric equivalent of the radiant emittance M is the luminous emittance M, measured in lm/m².
	The photometric equivalent of the radiant intensity I is the luminous intensity I. It is measured in lm/sr or candela. Candela was once known as the candle. The luminous intensity I was called the "candlepower". (A source with a uniform flux of 4π lm radiates 1 lm/sr or 1 candela. Hence, 4π or 12.57 lm of radiant flux from an isotropic source means that I = 1 cd. A typical 100-watt light bulb provides about 1,700 lm of visible energy. If the distribution were uniform, the luminous intensity I would be about 135 cd.)
	The photometric equivalent of the radiance L is the luminance L, measured in candela/m²or lm/sr/m². The luminance L is the property of a source that is commonly called "brightness". The unit for L used to be the Lambert.
	The photometric equivalent of the irradiance E is the illuminance E, measured in lm/m² = lux (lx).

If the energy supplied by dS is being received from another source and retransmitted isotropically, i.e. if dS is a perfect diffuser and its radiance or brightness is not a function of angle, then L = I/(dS cosθ) = I/dS_n = constant and I(θ) = LdS cos(θ) is related to its normal component I_n by the equation

I(θ) = I_n cosθ.

This is known as Lambert’s law. A surface which satisfies Lambert’s law is called Lambertian. Lambertian refers to a flat radiating surface. (The flat surface can be an elemental area of a curved surface.) A Lambertian surface can be an active surface or a passive, reflective surface. The intensity I(θ) falls off as the cosine of the observation angle with respect to the surface normal (Lambert's law). The radiance (W/(m²sr)) is independent of direction. A good example is a surface painted with a good "matte" or "flat" white paint. If it is uniformly illuminated, like from the sun, it appears equally bright from whatever direction you view it.

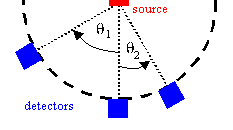
In the figure on the right, if the source is Lambertian and equally bright in all directions, then the amount of energy that falls each the detectors is not the same for each of the detectors, but depends on the angle θ as cosθ.
[Note: A source that is equally bright in all direction does not emit the same amount of energy in all directions. When determining the brightness of a small source we measure the energy that falls on a detector subtending a given solid angle at the source and then divide by the apparent size (area) of the source. A small source emitting the same amount of energy into the given solid angle as a larger source is brighter than the larger source.]

The apparent brightness of a Lambertian surface is the same when viewed from any angle. For a Lambertian surface only, we have the relation ship between the emittance M and the radiance L,

M = πL.

[L = d²P/(dΩ dS cosθ). If L is constant, then
M = dP/dS = ∫₀^π/2L cosθdΩ = 2πL∫₀^π/2cosθ sinθ dθ = πL.]

The ratio of the radiant emittance (W/m²) to the radiance (W/m²sr) of a Lambertian surface is a factor of π and not 2π. The radiance is integrated over a hemisphere. The factor of cos(θ) in the definition of radiance is responsible for this result. It is counterintuitive, since there are 2π steradians in a hemisphere.

Problem:

Consider a point P on a line normal to the center of a disk. The point is a distance a from the center of the disk, which has a radius R.

(a) Show that the solid angle subtended by the disk at the point is

(b) Show that, when the point P is very far from the disk, the solid angle reduces to zero.
(c) Show that, when P is very close to the disk, the solid angle becomes 2π.
(d) Show that when R/a << 1 the expression for Ω simplifies to Ω = πR²/a².
(e) Explain physically what (b), (c), and (d) mean.

Solution:

(a) Consider some surface S enclosing a point P. Now imagine a small cone, which intersects an infinitesimal area, dA, on S. The cone defines the solid angle subtended by the area dA at point P. By definition, the solid angle is the area dA projected on a plane perpendicular to the radius vector r from P to dA, and divided by r². If dΩ is the solid angle subtended by dA we have . The expression can be integrated over a region of S to find the total solid angle subtended by that region

Thus if the apex of a cone lies at the center of a sphere, the solid angle subtended is the ratio of the sphere surface area enclosed by the cone to the square of the radius of the sphere.

Since cosθ’ = a/(a²+r²)^1/2,we have

.

(b) If a goes to infinity, then a/(a²+r²)^1/2 goes to 1 and Ω = 2π(1 - 1) = 0.
(c) If P is very close to the disk, then a is very small compared to R. In zeroth order approximation we neglect the a/(a²+r²)^1/2 term and Ω = 2π. The cone encloses the surface area of half of a sphere.
(d) If R/a <<1 then we expand
.
Therefore Ω = πR²/a². The surface area of the sphere enclosed by the cone is so small that we can neglect its curvature and treat it as flat.

Problem:

A lens with a diameter of 1.25 in. and a focal length of 2.0 in. projects the image of a lamp capable of producing 3,000 cd/cm². Find the illuminance E in lm/ft²(footcandles) on a screen 20 ft from the lens.

Solution:

The focal length of the lens is f = 5.08 cm, the image distance is x_i = 609.6 cm, the object distance therefore is x_o = 5.12 cm. The magnification m = -609.9/5.12 = -119.19. The radius of the lens is R = 1.5875 cm.

The lens subtends a solid angle of Ω = 2πx_o(1/x_o – 1/(x_o²+R²)^1/2) sr = 0.282 sr at the lamp.

[In the figure on the right, the area of the spherical cap on a sphere with r is
∫₀^θ2πr²sinθ' dθ' = 2πr²(1 - cosθ), the solid angle Ω subtended by the cap is 2π(1 - cosθ).
For the lens cosθ = x_o/(x_o²+R²)^1/2.]

The radiant energy emitted per cm² into a solid angle 0.282 sr is 3000 times 0.282 = 845.6 lm.
This energy falls onto an area of m²*(1 cm²) = 14189.8 cm² on the screen. The illuminance E is therefore 0.0596 lm/cm², or 55.4 lm/ft².