

A basic refracting telescope is an optical instrument that has two optical elements, an objective and an eyepiece. We have two thin lenses in air. The objective is a large lens that collects light from a distant object and creates an image in the focal plane, which is a faithful representation of the object. The eyepiece is a sophisticated magnifying glass through which we view this image.
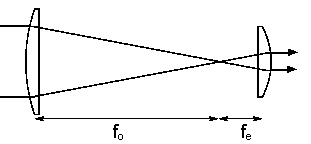
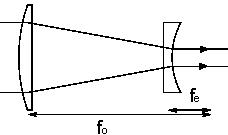
Keplerian telescope Galilean telescope
A Keplerian telescope has a converging lens eyepiece and a Galilean telescope has a diverging lens eyepiece. The distance between the image and the eyepiece is the sum of the focal lengths of the two lenses. (Remember that for a diverging lens the focal length is negative.) A telescope by itself is not an image forming system. The eye of the observer or the camera attached to the telescope forms the image.
We use a telescope to gather light and to increase the angle that a distant object subtends at the eye. If the eye is relaxed for distant viewing, the telescope simply produces an angular magnification. An incident (approximately) parallel beam from a distant source point, which makes an angle θ with respect to the optical axis, emerges as a parallel beam which makes a larger angle θ' with respect to the axis.
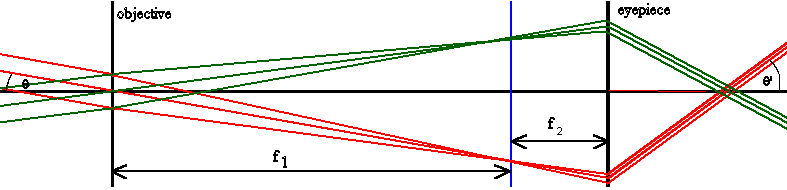
The transformation matrix for the Keplerian telescope is
 .
.
| Here
f1 is the focal length of the objective and f2 is the
focal length of the eyepiece. The telescopic system is characterized by M12
= 0.
The angular magnification is M11 = mθ
= -f1/f2,
it is the negative ratio of the focal length of the objective to the focal
lengths of the eyepiece.
The image as viewed through the Keplerian telescope is inverted, and the image formed by the objective lens is in the second focal plane of that lens which is also the first focal plane of the eyepiece lens. The image formed by the eyepiece is at infinity. The telescope is not an image forming system until we add another optical system, such as the lens of an eye or a camera. The angular magnification of a Galilean telescope is positive and the image is upright. |
(a)
(b)
A Keplerian (a) and a Galilean (b) telescope with the same angular magnification.
|
||||
| For a terrestrial telescope build with only converging lenses, one may insert an erector lens between the objective and eyepiece, such that the image formed by the objective acts as an object for the erector lens which in turn forms an inverted image at the first focal point of the eyepiece lens. The matrix of this system will have M12 = 0, and the angular magnification will be positive. |
|
||||
There are two basic types of telescopes:
|
Newtonian Reflecting Telescope
|
![]()
Problem:
A Galilean telescope has an objective lens with f1 = 20 cm and the eyepiece lens with f2 = -5 cm. The lenses are separated by 15 cm. Calculate the matrix for this system and find mθ.
| Solution: The lenses are separated by a distance f1 + f2. Therefore 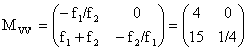 M11 = mθ = +4 is the angular magnification. |
![]()
Gathering as much light as possible is the principal function of astronomical telescopes. The larger the area π(D/2)2 of the objective the more light the telescope can collect. To compare the light gathering power (LGP) of two telescopes we compare the areas of their objectives. For the eye the objective is just the pupil, with a diameter of only ~0.8 cm.
The resolving power or resolution of a telescope is the smallest angular separation between two objects that can be seen. The smaller the resolving power of the telescope the better is the telescope. If two objects in the sky have a smaller angular separation than the resolving power of the telescope, the two objects will appear as one. However, if their angular separation is larger than the resolving power, then they will be resolved and appear as two distinct objects.
The resolution depends on the wavelength of the light entering the objective as well as on the diameter of the objective. The bigger the diameter of the objective the smaller the resolving power. For a telescope the theoretical intrinsic minimum angular separation is given by
θmin = 1.22 λ/D
where λ is the wavelength of the light and D the diameter of the objective. For the human eye and visible light D = 0.8 cm and λ = 500 nm, therefore θmin = 7.62*10-5 rad = 4.37*10-3 degree. Earth-bound telescopes rarely reach their theoretical resolution limit because of the blurring of the images due to atmospheric turbulence.
The magnifying power MP of a telescope is the (apparent) increase in the size of an object relative to its size when viewed with the unaided eye. MP is equal to the magnitude of the angular magnification mθ = -f1/f2. The ratio of the diameter of the entrance pupil to the exit pupil is also equal to MP. The magnifying power should be chosen so that the diameter of the exit pupil is approximately equal to the diameter of the pupil of the eye.
![]()
Microscopes
A compound microscope uses a simple combination of two converging lenses to produce a very effective magnifier. A sketch is shown below. The lens closest to the object is known as the objective, and the second lens is the eyepiece. The object is placed between fo and 2fo. An intermediate image is formed by the objective lens near the object focal plane of the eyepiece. The tube length g is the distance between the secondary focal point of the objective and the primary focal point of the eyepiece. The intermediate image serves as the object for the eyepiece.
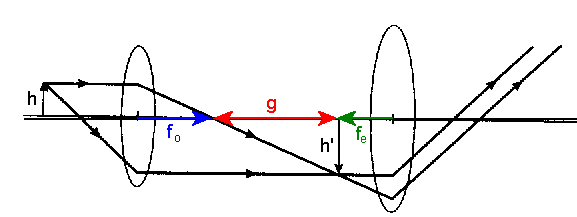
To have a tube length g an object distance xo satisfying 1/xo = 1/fo - 1/(g + fo) is needed. If the intermediate image is in the object focal plane of the eyepiece then the linear magnification of the objective is -g/f0 and and the angular magnification of the eyepiece is dv/fe. The total magnifying power of the microscope is given by MP = -g dv/(fofe) = -(g/fo)MPeyepiece. Here dv = 25 cm, the near point of the human eye. The focal lengths of both lenses should be extremely short to generate maximum angular magnification.
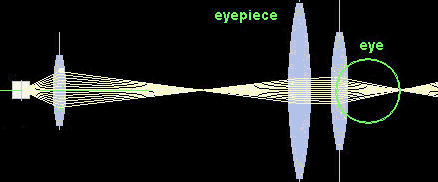
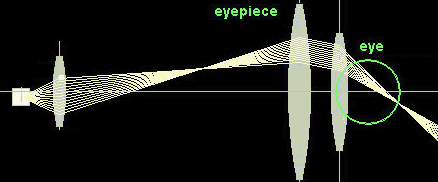
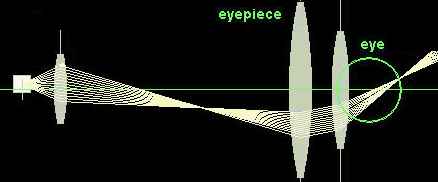
Illustration of the angular magnification of a microscope
Please explore
the
anatomy of a microscope