For mirrors, we must be careful with the sign conventions.  In the case of refraction, rays that move from left to right continue to move from left to right after refraction but in the case of reflection their course is reversed.  After reflection the rays move from right to left. 

Consider the figure above, depicting a concave spherical mirror.  Let us find an expression relating the angles θ_i and θ_r before and after reflection.

The law of reflection states that φ_i = φ_r.  From geometry we have

tan(θ_i - φ_i) ≈ θ_i – φ_i = -x_i/R.

For now we keep the sign convention for R that we use for refracting surfaces.  R is positive if the center of curvature C lies to the right of the vertex V and negative if C lies to the left of V.  This is the reverse of the convention we used in elementary optics for mirrors.

We find θ_r from θ_i = θ_r + 2φ_i and φ_i = ( θ_i - θ_r)/2.  These equations yield

θ_r = θ_i - 2φ_i = 2(θ_i - φ_i ) - θ_i,   or   θ_r = -θ_i - 2x_i/R

Multiplying by the index of refraction n of the surrounding medium we obtain

nθ_r = -n θ_i - 2nx_i/R.

We obviously have x_r = x_i, so the matrix for reflection becomes

,

using the above sign convention.

But in the matrix formulation it is perhaps easier to maintain all the sign conventions used for refraction and treat the reflected rays as having a slope angle equal to -θ_r, with θ_r given by the equation above.  This in effect allows us to treat the rays after reflection as if they were proceeding from left to right like the incoming rays.  Of course, if we then calculate a positive image distance or a positive focal length, the image and the focus will actually lie to the left of the reference point in a traditional ray diagram.

If we also keep the sign convention from elementary optics, and for mirrors let R be positive if it lies to the left of the vertex and negative if it lies to the right of the vertex, then the mirror matrix is then given by

.

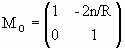The distance from the vertex to the focal point is f = R/2.