

Problem:
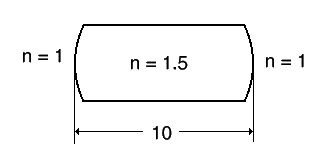
A thick biconvex lens in air has a radius of curvature of 10 cm at each surface and the surfaces are 10 cm apart. Find the focal points and the focal lengths of the lens if the index of the glass of the lens is 1.50.
|
Solution: |
For a thick lens we have for the transformation between the vertices
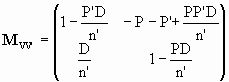
with P = (n'-n1)/R1 and P' = -(n'-n2)/R2. If
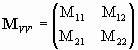
then the matrix for the transformation between the principal planes is
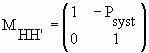 ,
,
with Psyst = -M12.
For a thick lens we therefore have
Psyst = (n'-n1)/R1 - (n'-n2)/R2 + D(n'-n1)(n'-n2)/(n'R1R2).Given the location of the principal planes we have
n1/S1 + n2/S2 = Psyst,
f' = n2/Psyst, f = n1/Psyst.
In our problem n1 = n2 = 1, n' = 1.5, R1 = 10 cm, R2 = -10 cm, D = 10 cm. We have f' = f = 1/Psyst, or
1/f = (n'-1)(1/R1 - 1/R2) + D(n'-1)2/(n'R1R2),
1/f = (0.5/5 - 10(0.5)2/150) cm-1, f = 12 cm.
Here f is the distance from the principal planes to the focal points. To find the distance from the vertex V to the focal point F we have to add D1 = n1P'D/(-Psystní) to f. To find the distance from the vertex V' to the focal point F' we have to add D2 = n2PD/(-Psystní) to f'.
D1 = -0.5f/1.5 = -(1/3)f, VF = 2/3f = 8 cm.
D2 = -0.5f'/1.5 = -(1/3)f, V'F' = 2/3f' = 8 cm.
F is 8 cm to the left of V, F ' is 8 cm to the right of V '.
![]()
Problem:
Let the lens be a biconcave thick lens with radii of 10 cm, index 1.5, thickness 1 cm. Show that f = f'= -9.84 cm, VF = -10.16 cm, V 'F ' = -10.16 cm.
|
Solution: |
In this problem n1 = n2 = 1, n' = 1.5, R1 = -10 cm, R2 = 10 cm, D = 1 cm. We have f' = f= 1/Psyst, or
1/f = (n'-1)(1/R1 - 1/R2) + D(n'-1)2/(n'R1R2),
1/f = (-0.5/5 - (0.5)2/150) cm-1, f = -9.84 cm.
D1 = P'D/(-Psystní), P'= -(n'-1)/R2, D1 = 0.5f/15, VF = 1.033f = -10.16cm.
D2 = PD/(-Psystní), P= (n'-1)/R2, D2 = 0.5f'/15, V'F' = 1.033f' = -10.16cm.
![]()
Problem:
A biconvex lens of index 1.50 has radii 10 cm and 20 cm, a thickness of 10 cm. Air is to the left of V and water (of index 4/3) is to the right of V '. Show that f' = 24 cm, f = 18 cm, V 'F ' = 16 cm, VF = 17 cm.
|
Solution: |
In this problem n1 = 1, n2 = 4/3, n' = 1.5, R1 = 10 cm, R2 = -20 cm, D = 10 cm.
Psyst = (n'-n1)/R1 - (n'-n2)/R2 + D(n'-n1)(n'-n2)/(n'R1R2),
Psyst = (0.05 + 0.00833 - 10(0.5)(0.01667)/300) cm-1 = 0.0556 cm-1.
f' = n2/Psyst = 4/(3Psyst) = 24 cm, f = n1/Psyst = 1/Psyst = 18 cm.
D1 = n1 P'd/(-Psystní), P' = -(n'-n2)/R2 = 0.00833 cm-1, D1 = -1 cm, VF = 17 cm.
D2 = n2Pd/(-Psystní), P = (n'-n1)/R1 = 0.05 cm-1, D2 = -8cm, VF = 16 cm.